ŠTATISTIKA PRAKTICKY (NIELEN) V ZÁVEREČNÝCH PRÁCACH
9. KOMPARÁCIA KVANTITATÍVNYCH PREMENNÝCH MEDZI NEZÁVISLÝMI VÝBERMI
Vo výskumoch sa bez komparácie málokedy zaobídeme, pretože veľmi často je jednou z premenných, medzi ktorými sledujeme súvislosti, kategorická premenná (pohlavie, vekové skupiny, typ študijného odboru, typ rodiny a pod.) a druhou je kvantitatívna premenná (merané hodnoty z dotazníkov, testov, čas a pod., čiže kardinálne či ordinálne premenné). Súvislosť sa v tomto prípade dá zistiť tým, že budeme predpokladať rozdielne hodnoty medzi skupinami, ktoré sú definované kategorickou premennou. Napríklad, môžeme predpokladať, že ženy budú mať vyššie skóre v dotazníku empatie než muži, čo vecne, laicky svedčí o súvislosti medzi empatiou a pohlavím.
Skupiny, ktoré porovnávame môžu byť DVE alebo 3 A VIAC, osobitným typom je porovnanie ZÁVISLÝCH VÝBEROV (1. a 2., prípadne 3. a ďalšie meranie rovnakej premennej v jednom a tom istom súbore), ktoré je predmetom spracovania v kapitole 11. Pre každú alternatívu existujú rôzne parametrické a neparametrické testy. Voľba PARAMETRICKÉHO či NEPARAMETRICKÉHO testu závisí predovšetkým od typu porovnávanej premennej, teda či ide o kardinálnu alebo ordinálnu. Parametrické testy sú uspôsobené pre kardinálne premenné, ktoré by mali spĺňať vo všetkých porovnávaných skupinách kritérium normálneho rozdelenia (musí sa predtým testovať normalita vo všetkých skupinách, ktoré sa porovnávajú), pretože pracuje na princípe porovnania priemerov. Neparametrické testy pracujú na princípe porovnania poradí (Walker, 2010) a sú vhodné pre prácu s ordinálnymi či nie normálne rozdelenými kardinálnymi premennými. Podrobnejšie pravidlá pri výbere štatistického testu nájdete v kapitole 6.
9.1 Komparácia kvantitatívnej premennej medzi 2 skupinami (2 nezávislé výbery)
V aktuálnej časti sa budeme venovať komparačným testom 2 nezávislých výberov, teda príkladom, kde určitú kvantitatívnu premennú porovnávame medzi dvoma skupinami.
- Pokiaľ je porovnávaná premenná kardinálna (K), prvým krokom je testovanie normality, ktoré je potrebné vykonať v oboch skupinách samostatne15. Ak je premenná v oboch skupinách normálne rozdelená (aspoň podľa Shapiro-Wilkovho testu), môžeme použiť parametrický test – STUDENTOV T-TEST, pokiaľ nie, použije sa neparametrický – MANN-WHITNEYHO U TEST.
- Pokiaľ porovnávame ordinálnu premennú (O), priamo použijeme neparametrický test, teda MANN-WHITNEYHO U TEST.
V oboch variantoch testov (parametrickom i neparametrickom) sa štatistická interpretácia opiera o:
- zhodnotenie štatistickej významnosti Sig.:
- pokiaľ táto je menšia ako stanovená hladina α (štandardne 0,05), rozdiel je významný (Sig. < 0,05),
- interpretuje sa ďalej smerovanie rozdielu, teda v ktorej skupine je vyššie/nižšie skóre (v parametrickom podľa priemerov, v neparametrickom podľa priemerných poradí).
- pokiaľ je Sig. > 0,05, rozdiel nie je významný, na výskumnú otázku (Existuje rozdiel v…. medzi…?) odpovedáme záporne, alebo zamietame hypotézu o rozdiele
- pokiaľ táto je menšia ako stanovená hladina α (štandardne 0,05), rozdiel je významný (Sig. < 0,05),
A. PARAMETRICKÉ TESTOVANIE
Príklad 2:
H3: Predpokladáme, že existuje rozdiel v Neurotizme medzi ženami a mužmi.
Ekvivalenty:
H3a (dvojsmerná): Predpokladáme, že v škále Neurotizmus meranej BFI -44 bude rozdiel vzhľadom na pohlavie .
H3b (jednosmerná): Predpokladáme, že dievčatá budú dosahovať vyššie hodnoty v škále Neurotizmus (BFI -44) než chlapci.
V prípade hypotéz H3a a H3b sme na základe splnenia kritéria normality premennej Neurotizmus v oboch skupinách zvolili parametrický test: Studentov t-test pre 2 nezávislé výbery.
V SPSS je príkaz nasledovný:
- ANALYZE/ COMPARE MEANS/ INDEPENDENT-SAMPLES T-TEST, po otvorení okna je potrebné do časti TEST VARIABLE(S) presunúť porovnávanú premennú16 a do GROUPING VARIABLE preniesť tú kategorickú premennú, ktorá súbor rozdeľuje na skupiny. Po vložení premennej rozklikneme /DEFINE GROUPS, kde je potrebné ešte uviesť hodnoty (kódy 17) pre Group 1 a Group 2. V tomto prípade 1 (ženy) a 2 (muži)18.
Výstup z programu obsahuje tabuľku s deskripciou a druhú tabuľku, kde nájdeme v ľavej časti výsledok Levenovho testu rovnosti rozptylov a v pravej časti výsledok samotného Studentovho t-testu . Tabuľka je trochu komplikovanejšia.
- Levenov test testuje, či sú rozptyly (Variances) v oboch skupinách homogénne čo je podmienka pre realizáciu Studentovho t-testu. Pri Levenovom teste nás zaujíma príslušná Sig., ktorá, ak je Sig. > 0,05, skupiny sú homogénne.
- Toto je dôležité pre ďalší postup:
- ak je homogenita dodržaná (Equal variances assumed), interpretujeme ďalej výsledok prvého riadku samotného t-testu.
- ak dodržaná nie je (Equal variances not assumed), relevantný je pre nás druhý riadok výsledkov t-testu, ktorý je pri nehomogenite vypočítaný iným spôsobom, než klasický t-test, preto sa výsledky v dvoch riadkoch môžu líšiť.
Tabuľky odporúčame integrovať do jednej a zachovať v nej údaje potrebné pre interpretáciu výsledkov pre nami stanovenú hypotézu (Tabuľka 10).
Interpretácia výsledku testovania:
Predpoklad bol overovaný Studentovým t- testom. Levenov test potvrdil homogenitu rozptylov (Sig. > 0,05), preto ďalej interpretujeme prvý riadok výsledkov t- testu (t = -4,076; Sig. < 0,001). Rozdiel v priemeroch (-2,3) medzi skupinami interpretujeme ako štatisticky významný. Medzi mužmi a ženami existuje významný rozdiel v skóre Neurotizmu. Hypotézu H3 (rovnako H3a) prijímame. (Táto interpretácia postačuje,ak je hypotéza dvojsmerná.)
Ak je jednosmerná, po zistení významného rozdielu (ak by bola Sig. > 0,05, hypotézu priamo zamietneme) sledujeme ďalej aj hodnoty priemerov a určujeme, v ktorej skupine (v ktorom riadku) sú vyššie či nižšie:
Na základe priemerných poradí evidujeme vyššie hodnoty Neurotizmu u žien (AM = 27,3) než u mužov (AM = 25,0). Hypotézu H3b prijímame.
Na zobrazenie rozdielov je vhodný error bar (Graf 9), v ktorom je zobrazený 95% interval spoľahlivosti výskytu hodnôt (úsečne) a aritmetický priemer ako krúžok uprostred.
Tabuľka 10 Výsledky testovania H3: Studentov t-test
| Pohlavie | N | Priemer | Štd.odchýlka | |
| Neurotizmus | Muži | 256 | 25,0 | 6,12 |
| Ženy | 245 | 27,3 | 6,63 |
| Levenov test rovnosti rozptylov | t-test rovnosti priemerov | |||||
| Homogenita rozptylov | F | Sig. | t | df | Sig. | Priemerný rozdiel |
| Predpokladaná | 2,198 | ,139 | -4,076t | 499 | ,000 | -2,3 |
| Nepredpokladaná | -4,069 | 491,4 | ,000 | -2,3 | ||
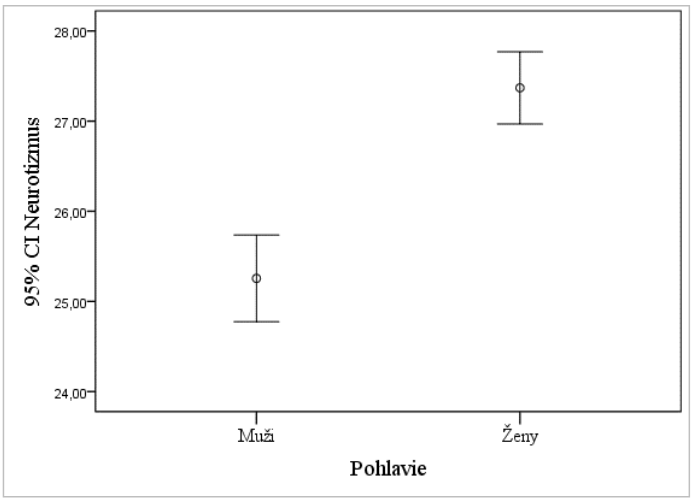
Graf 9 Error bar pre zobrazenie rozdielu v premennej Neurotizmus medzi skupinami mužov a žien
B. NEPARAMETRICKÉ TESTOVANIE
Neparametrické testovanie použijeme, ak porovnávame dve skupiny respondentov (rozdelené podľa nejakej kategorickej premennej) v kvantitatívnej ordinálnej premennej alebo kardinálnej premennej, ktorá nespĺňa kritériá pre použitie parametrického testu.
Test pracuje na princípe porovnávania poradí, do ktorých usporiada respondentov jednej a druhej skupiny podľa ich dosiahnutých reálnych hodnôt premennej. Rozdiel je potom počítaný medzi výslednými priemernými poradiami (MEAN RANKs, sú zobrazené v prvej tabuľke v output okne SPSS), z čoho sú generované výsledky Mann-Whitneyho U testu: U, Z a príslušná štatistická významnosť (Assymp.Sig) (druhá tabuľka výsledkov v SPSS)19 V prezentácii výsledkov odporúčame tabuľky zlúčiť do jednej, s uvedením len relevantných hodnôt, ako je to je zobrazené v tabuľke (Tabuľka 11)
Príklad 4:
H4: Predpokladáme, že adolescenti, ktorí experimentovali s marihuanou a tí, ktorí ešte neskúšali marihuanu sa líšia v hodnotení pocitu bezpečia doma (dvojsmerná).
Ekvivalenty:
H4a (dvojsmerná): Predpokladáme, že existuje rozdiel v pocite bezpečia doma vzhľadom na experimentovanie s marihuanou .
H4b (jednosmerná): Predpokladáme, že adolescenti, ktorí experimentovali s marihuanou uvádzajú nižšie hodnoty pocitu bezpečia doma ako adolescenti, ktorí s marihuanou doteraz neexperimentovali.
- Premenná „Pocit bezpečia doma“ je ordinálna premenná, dosahuje 4 hodnoty, pričom 1 = Vôbec nie je pravda, …, 4 = Úplná pravda.
- Premenná „Experimentovanie s marihuanou“ je binárna, dosahuje hodnoty 0 = NIE a 1 = ÁNO
V SPSS volíme test nasledovne:
- ANALYZE/ NONPARAMETRIC TESTS/ LEGACY DIALOGS/ 2 INDEPENDENT SAMPLES. V otvorenom dialógovom okne presunieme do hornej časti TEST VARIABLE LIST premennú (alebo viaceré naraz), ktoré chceme porovnať, pričom musí to byť ordinálna alebo kardinálna premenná (tu „Pocit bezpečia doma“), do dolného okna vložíme premennú, ktorá nám rozdeľuje súbor do porovnávaných skupín (GROUPING VARIABLE, v tomto prípade „Experimentovanie s marihuanou“) – musíme rozkliknúť /DEFINE GROUPS, kde zadáme hodnoty (označenia), ktorými sú zakódované skupiny v databáze (v tomto prípade 1 a 020).
Interpretácia výsledku testovania:
Predpoklad bol overovaný Mann-Whitneyho U testom s výsledkom U = 514867,0; Z = -6,792; Sig. < 0,001. Rozdiel v priemerných poradiach medzi skupinami interpretujeme ako štatisticky významný. Medzi adolescentmi vzhľadom na experimentovanie s marihuanou existuje významný rozdiel v hodnotách premennej
Pocit bezpečia doma. Hypotézu H4 (rovnako H4a) prijímame. (Táto interpretácia postačuje,ak je hypotéza dvojsmerná.)
Ak je jednosmerná, po zistení významného rozdielu (ak by bola Sig. > 0,05, hypotézu priamo zamietneme) sledujeme ďalej aj hodnoty priemerných poradí a určujeme, v ktorej skupine (v ktorom riadku) sú vyššie či nižšie:
Na základe priemerných poradí evidujeme vyššie hodnoty Pocitu bezpečia doma u adolescentov, ktorí neexperimentovali s marihuanou (MR = 1277,7) než u adolescentov, ktorí už s marihuanou experimentovali (MR = 1114,8). Hypotézu H4b prijímame.
Tabuľka 11 Výsledky testovania H4: Mann-Whitneyho U test
| Experim. s marihuanou | N | Priemerné poradie | Mann-Whitneyho test | ||
| Pocit bezpečia doma | ÁNO | 1814 | 1277,7 | U | 514867,0 |
| NIE | 654 | 1114,8 | Z | -6,792 | |
| Spolu | 2468 | Sig. | ,000 | ||
Na zobrazenie rozdielov je vhodný boxplot, v ktorom je zobrazený rozsah hodnôt, 1. a 3. kvartil, medián (v strede boxu), hraničné a extrémne hodnoty (krúžky, hviezdičky), ktoré sa vymykajú 95% intervalu spoľahlivosti. Pri ordinálnych premenných môže byť vygenerovaný aj takýto zvláštny typ boxplotu ( Graf 10).
Interpretácia grafu:
V uvedenom grafe pre skupinu, ktorá neexperimentovala s marihuanou (NIE) je celý box „skrytý“ v jednej úsečke, čo znamená, že medián, 1. i 3. kvartil sú na jednej hodnote 4. Prakticky to znamená, že minimálne 75% respondentov z tejto skupiny odpovedalo najvyššou hodnotou, ostatné hodnoty sú vyznačené ako hviezdičky, program ich vyhodnotil ako extrémne. V druhej skupine môžeme vidieť, že taktiež medián, ale i tretí kvartil sú na hodnote 4 (minimálne 50% respondentov označilo túto hodnotu), 1.kvartil na hodnote 3 a ohraničenie 95 intervalu spoľahlivosti na hodnote 2.Taktiež vidíme niekoľko hraničných hodnôt označených krúžkami, tieto sú menej vzdialené „boxu“ než extrémy (hviezdičky).
DÔLEŽITÉ: V grafe môžeme vidieť pri hviezdičkách a krúžkoch aj číselné hodnoty. Je potrebné si uvedomiť, že tieto hodnoty znamenajú poradové číslo prípadu (ktorý vykazuje túto hodnotu) v databáze (DATA VIEW) a nie samotnú extrémnu či hraničnú hodnotu!!! Hodnoty máme na osi Y.
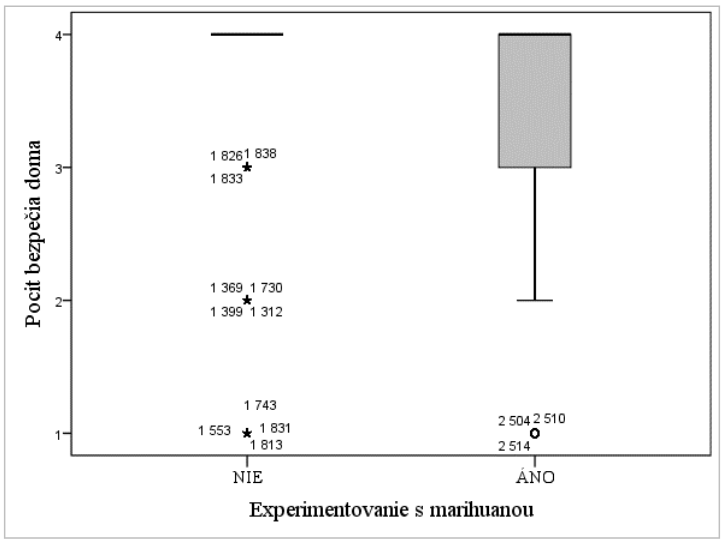
Graf 10 Boxploty zobrazujúce deskriptívne parametre premennej Depresívne symptómy v skupinách mužov a žien
9.2 Komparácia kvantitatívnej premennej medzi 3 alebo viac skupinami
Komparačné testy pre porovnanie kvantitatívnej premennej medzi 3 a viac výbermi uplatňujeme, pokiaľ niektorá zo skúmaných premenných je kategorická/kvalitatívna, má viac ako 2 kategórie a sledujeme jej súvislosti s druhou premennou, ktorá je kvantitatívna (ordinálna či kardinálna). Kategorická premenná rozdeľuje súbor na skupiny (3 alebo viac), medzi ktorými sa zisťuje rozdiel v druhej premennej, teda, či je v niektorej skupine vyššie, nižšie, najnižšie štatisticky rozdielne skóre, hodnota kvantitatívnej premennej. Na základe štatisticky významných rozdielov v kvantitatívnej premennej medzi skupinami vecne interpretujeme súvislosť medzi premennými.
Napríklad, súvislosť medzi študijným odborom na vysokej škole a mierou empatie. Budeme predpokladať, že empatia bude významne vyššia u študentov psychológie (1. skupina) v porovnaní so študentmi matematiky (2. skupina) a masmediálnej komunikácie (3. skupina).
Rovnako, ako pri porovnaní 2 skupín, pre parametrické a neparametrické testovanie existujú rôzne štatistické testy. Parametrické porovnanie 3 a viac výberov: ONE-WAY ANOVA; neparametrické porovnanie 3 a viac výberov: KRUSKAL WALLISOV TEST. Interpretácia oboch, podobne ako pri porovnaní 2 skupín, sa opiera o:
- zhodnotenie štatistickej významnosti Sig. :
- pokiaľ táto je menšia ako stanovená hladina α (štandardne 0,05), rozdiel je významný (Sig. < 0,05),
- interpretuje sa ďalej smerovanie rozdielu, teda v ktorej skupine je vyššie/nižšie skóre (v parametrickom podľa priemerov alebo podľa výsledku POST HOC testu, v neparametrickom podľa priemerných poradí).
- pokiaľ je Sig. > 0,05, rozdiel nie je významný, na výskumnú otázku (Existuje rozdiel v…. medzi…?) odpovedáme záporne, alebo zamietame hypotézu o rozdiele.
- pokiaľ táto je menšia ako stanovená hladina α (štandardne 0,05), rozdiel je významný (Sig. < 0,05),
A. PARAMETRICKÉ TESTOVANIE
Príklad 5:
H5 (výskumná hypotéza) : Predpokladáme, že existuje súvislosť medzi životnou spokojnosťou a stupňom ukončeného vzdelania .
Ekvivalenty:
H5a (obojsmerná): Predpokladáme, že existujú rozdiely v životnej spokojnosti vz hľadom na dosiahnuté vzdelanie.
H5b (jednosmerná): Predpokladáme, že vysokoškolsky vzdelaní respondenti budú mať vyššiu životnú spokojnosť než respondenti so stredoškolským (a vyšším odborným vzdelaním) alebo zo základným vzdelaním.
V prípade hypotéz H5a a H5b sme, na základe splnenia kritéria normality premennej Životná spokojnosť vo všetkých troch skupinách, zvolili parametrický test: Jednosmernú analýzu rozptylu (ONE-WAY ANOVA).
V SPSS je príkaz nasledovný:
- ANALYZE/ COMPARE MEANS/ ONE-WAY ANOVA, po otvorení príkazového okna je potrebné do časti DEPENDENT LIST presunúť porovnávanú premennú21 a do FACTOR22 preniesť tú kategorickú premennú, ktorá súbor rozdeľuje na skupiny (v tomto prípade „Stupeň vzdelania“). ANOVA sama negeneruje deskriptívnu tabuľku, preto ak ju chceme, musíme rozkliknúť /OPTIONS a zaškrtnúť DESCRIPTIVE, tiež tu môžeme zadať aj MEAN PLOT, čo je čiarový graf zobrazujúci priemerné hodnoty v skupinách.
Po uvedenom zadaní SPSS vygeneruje dve tabuľky. V prvej sú deskriptívne ukazovatele (N, priemer, ŠO, interval spoľahlivosti, Min, Max). V druhej tabuľke, ktorú, už upravenú, prezentujeme nižšie (Tabuľka 12), je výsledok ANOVA testu s hodnotami F a Sig. dôležitými pre interpretáciu.
V prípade jednosmernej hypotézy (H5b) je pre interpretáciu potrebné poznať presné štatistické významnosti rozdielov medzi dvojicami skupín a nielen významnosť celkového porovnania (ktoré generuje vyššie uvedený postup), pretože by sme nedokázali určiť, či medzi jednou a ostatnými dvoma skupinami je významný rozdiel (ako máme určené v hypotéze). V takom prípade po otvorení dialógového okna One-Way ANOVA a presunutí dependent a factor premenných, je potrebné rozkliknúť /POST HOC a zvoliť typ tzv. „multiple comparison“ – testu mnohonásobného porovnania. V literatúre nájdeme odporúčania zvoliť (zaškrtnúť) LSD alebo TUKEY-ho test (Sollár, Ritomský, 2002; Coolican, 2014). Vo výstupe potom nájdeme samostatnú tabuľku s výsledkom „multiple comparison“ testu, ktorú v prácach môžeme upraviť a prezentovať spôsobom, ako je to znázornené v tabuľke (Tabuľka 13).
Interpretácia výsledku testovania:
Výsledky testovania hypotézy H5a/H5b uvádzame v tabuľkách (Tabuľka 12, Tabuľka 13). Na overenie bola použitá jednosmerná analýza rozptylu (ANOVA) s výsledkom: F = 2,635; Sig. > 0,05. Vzhľadom na hodnotu štatistickej významnosti, ktorá je väčšia ako stanovené kritérium, hypotézu H5a/H5b o rozdiele medzi skupinami zamietame. Medzi skupinami podľa dosiahnutého stupňa vzdelania neexistuje štatisticky významný rozdiel v životnej spokojnosti. Pokiaľ rozdiel celkovo medziskupinovo (podľa ANOVY) nie je významný, platí to pre jednosmernú i dvojsmernú hypotézu. Ak by bola Sig. < 0,05, interpretujeme aj výsledky POST HOC testu23
Tabuľka 12 Výsledky testovania H5a a H5b: One-Way ANOVA
| Súčet štvorcov | df | Priemerný štvorec | F | Sig. | ||
| Životná spokojnosť * Stupeň dosiahnutého vzdelania | Medziskupinovo | 239,7 | 2 | 119,8 | 2,635 | 0,73 |
| Vnútroskupinovo | 19694,9 | 433 | 45,5 | |||
| Spolu | 19934,6 | 435 |
Príklad interpretácie POST HOC testu, pokiaľ by to bolo relevantné (výsledok ANOVY by hovoril o významnom rozdiele, Sig. < 0,05):
V tabuľke (Tabuľka 13) uvádzame výsledky Post Hoc LSD testu, kde v poslednom stĺpci sú uvedené štatistické významnosti Sig. pre parciálne porovnania dvojíc skupín. Významný rozdiel interpretujeme, pokiaľ Sig. < 0,05, čo evidujeme v tomto prípade pri porovnaní skupiny so stredoš kolským a vyšším odborným vzdelaním so skupinou s vysokoškolským vzdelaním. Rozdiel v tomto poradí porovnania „Skupina v stĺpci A – Skupina v stĺpci B“ = – 1,560, ide o zápornú hodnotu, čo značí, že životná spokojnosť v skupine s vysokoškolským vzdelaním dosahuje vyššie hodnoty než v skupine so stredoškolským a vyšším odborným vzdelaním, tento rozdiel je významný (Sig. < 0,05). V ostatných parciálnych porovnaniach dvojíc skupín neevidujeme významné rozdiely. Hypotézu H5b by sme tak či tak zamietli, pretože predpokladala najvyššiu životnú spokojnosť u vysokoškolsky vzdelaných respondentov v porovnaní s oboma skupinami, avšak rozdiel medzi skupinou s vysokoškolským a skupinou so základným vzdelaním nie je významný.
Tabuľka 13 Viacnásobné porovnanie v rámci testovania H5b: LSD test24
| Kategórie vzdelania | Priemerný rozdiel | Štd.chyba | Sig. | ||
| A | B | A-B | |||
| Životná spokojnosť | Základné | Stredošk., vyššie odb. | 1,2 | 1,0 | ,268 |
| Vysokoškolské | -0,4 | 1,1 | ,692 | ||
| Stredošk., vyššie odb. | Základné | -1,2 | 1,0 | ,268 | |
| Vysokoškolské | -1,6 | 0,7 | ,025 | ||
| Vysokoškolské | Základné | 0,4 | 1,1 | ,692 | |
| Stredošk., vyššie odb. | 1,6 | 0,7 | ,025 |
Výsledky ANOVA testu je vhodné znázorniť buď mean plot-om (Graf 11, zadáva sa v ANOVA pod /OPTIONS), error bar-om (ako pri t-teste, pozri vyššie) alebo v Exceli čiarovým grafom.
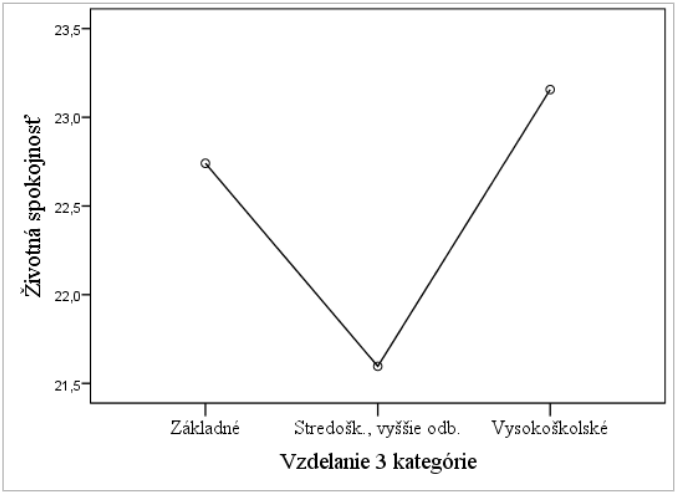
Graf 11 Mean plot pre zobrazenie Životnej spokojnosti v troch skupinách vzhľadom na dosiahnutý stupeň vzdelania
B. NEPARAMETRICKÉ TESTOVANIE
KRUSKAL WALLISOV TEST je neparametrický porovnávací test pre 3 a viac výberov. Použijeme ho, pokiaľ porovnávame kvantitatívnu premennú (ordinálnu, alebo kardinálnu, ktorá nespĺňa kritériá pre parametrické testovanie) medzi 3 či viac skupinami.
Test pracuje na princípe porovnávania poradí (rovnako ako Mann-Whitneyho U test), do ktorých usporiada respondentov každej skupiny podľa ich dosiahnutých reálnych hodnôt premennej. Rozdiel je potom počítaný medzi výslednými priemernými poradiami (Mean Ranks, prvá tabuľka z SPSS), z čoho sú generované výsledky Kruskal Wallisovho testu: χ2 , stupne voľnosti (df) a príslušná štatistická významnosť (Assymp.Sig) (druhá tabuľka z SPSS). Relevantné výsledky z výstupov zo štatistického testovania je možné v prácach prezentovať v jednej tabuľke, ako je to znázornené v tabuľke (Tabuľka 14).
Príklad 6:
H6: Predpokladáme, že žiaci rôznych typov škôl sa významne líšia v Pozitívnom vzťahu ku škole (dvojsmerná).
Ekvivalenty:
H6a (dvojsmerná): Predpokladáme, že existuje rozdiel v Pozitívnom vzťahu ku škole vzhľadom na typ strednej školy .
H6b (jednosmerná): Predpokladáme, že gymnazisti budú mať pozitívnejší vzťah ku škole než žiaci iných typov stredných škôl .
H6c (jednosmerná): Predpokladáme, že žiaci zo SOU budú vykazovať najnižšie skóre Pozitívneho vzťahu ku škole v porovnaní so žiakmi z gymnázií a zo SOŠ.
V SPSS volíme test nasledovne:
- ANALYZE/ NONPARAMETRIC TESTS/ LEGACY DIALOGS/ K INDEPENDENT SAMPLES. V otvorenom dialógovom okne presunieme do časti TEST VARIABLE LIST premennú (alebo viaceré naraz), ktorú chceme porovnať, pričom musí to byť ordinálna alebo kardinálna premenná (tu „Pozitívny vzťah ku škole“ je kardinálna premenná bez normálneho rozdelenia), do spodnej časti GROUPING VARIABLE vložíme premennú, ktorá rozdeľuje súbor do porovnávaných skupín (v tomto prípade „Typ školy“), ďalej musíme rozkliknúť /DEFINE GROUPS, kde zadáme kódy (označenia), ktorými sú označené skupiny kategorickej rozdeľujúcej premennej, na rozdiel od príkazu v Mann-Whitneyho teste tu ale volíme interval hodnôt, napr. skupiny 1-3, 1-4, 2-5 a podobne25.
Interpretácia výsledku testovania:
Predpoklad bol overovaný Kruskal Wallisovým testom s výsledkom χ2 = 17,294 pri df = 2 ; Sig. < 0,001 (Tabuľke 14), na základe ktorého interpretujeme rozdiely v priemerných poradiach medzi skupinami ako štatisticky významné. Medzi žiakmi rôznych typov stredných škôl existuje významný rozdiel v skóre premennej Pozitívny vzťah ku škole. Hypotézu H6 o rozdiele (rovnako H6a) prijímame.
(Táto interpretácia postačuje, ak je hypotéza dvojsmerná.)
Ak je jednosmerná, po zistení významného rozdielu (tzn. Sig. < 0,05. Ak by bola Sig. > 0,05, hypotézu priamo zamietneme) sledujeme ďalej aj hodnoty priemerných poradí a určujeme, v ktorej skupine (v ktorom riadku) je najvyššie či najnižšie:
Na základe priemerných poradí evidujeme najvyššie hodnoty Pozitívneho vzťahu ku škole u žiakov z gymnázií (MR = 201,7) a najnižšie u žiakov zo SOŠ (MR = 74,2). Hypotézu H6b (rovnako H6c) prijímame, nakoľko gymnazisti majú významne pozitívnejší vzťah ku škole než žiaci z iných škôl. (Žiaci zo SOU majú vzťah ku škole najmenej pozitívny v porovnaní s ostatnými dvoma typmi škôl.)
Tabuľka 14 Výsledky testovania H6: Kruskal Wallisov test
| Typ školy | N | Priemerné poradie | Kruskal Wallisov test | ||
| Pozitívny vzťah ku škole | Gymnázium | 224 | 201,7 | Chi-kvadrát | 17,294 |
| SOŠ | 140 | 164,3 | df | 2 | |
| SOU | 26 | 74,2 | Sig. | ,000 | |
| Spolu | 370 | ||||
Rovnako na znázornenie rozdielov slúži graf boxplot (bude mať tri boxy = tri skupiny), avšak tieto musíme najskôr v tomto konkrétnom prípade vyselektovať príkazom SELECT CASES 26 (pretože premenná Typ školy má až 7 kategórií a my potrebujeme len tri).
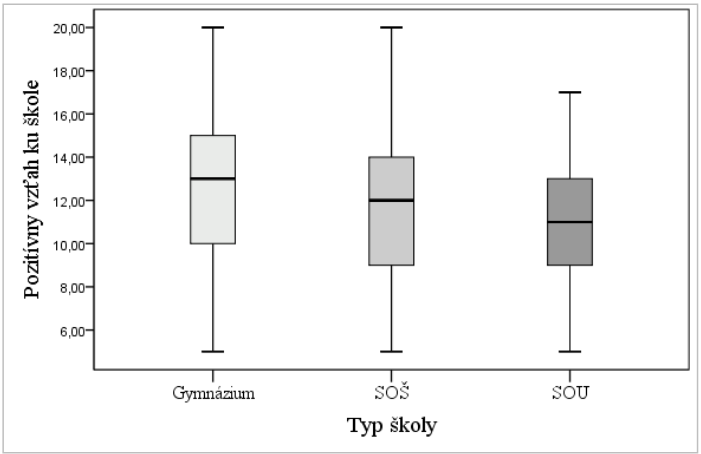
Graf 12 Boxploty zobrazujúce deskriptívne parametre premennej Pozitívny vzťah ku škole v troch skupinách podľa typu školy
ÚLOHY
- Sformulujte dvojsmernú a potom i jednosmernú hypotézu na súvislosť medzi
adrenalínovým športovaním (N) a úzkostlivosťou (K).
- Uvažujte, ako by boli premenné operacionalizované (vymyslite spôsob merania, definovania).
- Aké parametre musíme zohľadniť pri voľbe testu? Medzi akými testami by ste sa rozhodovali?
- Rozmýšľajte:
- aké rôzne premenné môžu diferencovať súbor na 3 a viac porovnateľných skupín.
- aké ordinálne premenné by bolo možné medziskupinovo porovnávať.
- Sformulujte jednosmernú komparačnú hypotézu o rozdiele v kvantitatívnej (K, O)
premennej medzi dvoma či viac skupinami.
- Zohľadnite potrebné parametre (normalita, štandardnosť testu, veľkosť vzorky) a zvoľte typ štatistické testu.
- Hypotézu otestujte (v SPSS), výsledky spracujte do tabuľky a interpretujte.
- Výsledok zobrazte príslušným grafom

