ŠTATISTIKA PRAKTICKY (NIELEN) V ZÁVEREČNÝCH PRÁCACH
10.KOMPARÁCIA VIACERÝCH MERANÍ PREMENNEJ V ROVNAKOM SÚBORE
Ide o principiálne inú komparáciu, než tie, ktoré sme popísali v predchádzajúcich podkapitolách. Neporovnávame tu skupiny, ale dve rôzne premenné, ktoré reprezentujú ten istý jav s odstupom času. Ide o viacnásobné merania rovnakého javu v tom istom súbore respondentov, ktoré sa využíva v experimentoch (meranie PRED a PO pôsobení podnetu) a v longitudinálnych výskumoch (meranie tej istej kohorty po určitých časových intervaloch). Premenné jednotlivých meraní sa do databázy zapisujú ako samostatné premenné, tzn. do samostatných stĺpcov a označujú sa ako Meranie 1, Meranie 2, Meranie 3… Takéto merania sa v SPSS nazývajú ako „paired samples“ alebo „related samples“, pretože každý respondent má v databáze priradené postupne v stĺpcoch hodnoty zo všetkých meraní, hodnoty sú teda spárované.
V rámci párových testov rozlišujeme testy:
- podľa typu premennej:
- pokiaľ ide o kardinálnu premennú, ktorá vo všetkých meraniach vykazuje normálne rozdelenie, volíme parametrický test.
- v prípade ordinálnej premennej alebo kardinálnej, ktorá aspoň v jednom meraní nespĺňa kritérium normality, volíme neparametrický test.
- podľa počtu meraní:
- na testy pre 2 merania: param. PAIRED SAMPLES T-TEST; neparam. WILCOXONOV SIGN-RANK TEST;
- testy pre 3 a viac meraní: param. REPEATED MEASURES ANOVA; neparam, FRIEDMANOV TEST.
10.1 Komparácia 2 závislých výberov
Ako sme už spomenuli vyššie, testy v rámci komparácie 2 meraní rovnakej premennej v rovnakom súbore sa líšia podľa typu premennej a princíp zisťovania rozdielov je rôzny v parametrickom a neparametrickom testovaní. Interpretácia sa však v oboch prípadoch opiera o:
- zhodnotenie štatistickej významnosti Sig. :
- pokiaľ táto je menšia ako stanovená hladina α (štandardne 0,05), rozdiel je
významný (Sig. < 0,05),- interpretuje sa ďalej smerovanie rozdielu, teda v ktorom meraní sú vyššie/nižšie hodnoty (v parametrickom podľa priemerov, v neparametrickom podľa priemerných poradí alebo počtu kladných/záporných rozdielov na úrovni jednotlivcov).
- pokiaľ je Sig. > 0,05, rozdiel nie je významný, na výskumnú otázku (Existuje rozdiel medzi prvým meraním… a druhým meraním? Došlo k významnému zlepšeniu v…. v priebehu času?) odpovedáme záporne, alebo zamietame hypotézu o rozdiele medzi meraniami.
- pokiaľ táto je menšia ako stanovená hladina α (štandardne 0,05), rozdiel je
A. PARAMETRICKÉ TESTOVANIE
Normálne rozdelené kardinálne premenné dvoch meraní javu v tom istom súbore je možné porovnať parametricky, pričom ako základ pre výpočet slúži rozdiel v stredných hodnotách (Mean Difference) medzi prvým a druhým meraním, výsledky testu obsahujú hodnotu t, stupne voľnosti (df) a príslušnú štatistickú významnosť (Sig.). Niekoľko tabuliek generovaných v SPSS je možné zlúčiť do jednej (Tabuľka 15).
Príklad 7:
H7 (výskumná dvojsmerná): Predpokladáme, že interakčné učenie má efekt
na sebadôveru.
Ekvivalenty:
H7a (dvojsmerná): Predpokladáme, že medzi meraním pred aplikáciou interakčného učenia a meraním po aplikácii interakčného učenia budú významné rozdiely v sebadôvere.
H7b (jednosmerná): Predpokladáme, že medzi meraním pred aplikáciou interakčného učenia a po jeho aplikácii dôjde k významnému zlepšeniu sebadôvery (nárast hodnôt).
Pri testovaní normality premennej Sebadôvera PRED a Sebadôvera PO bolo normálne rozdelenie v oboch prípadoch potvrdené. Na testovanie rozdielov medzi meraniami použijeme parametrický PAIRED-SAMPLES T-TEST (t-test pre dva závislé výbery).
V SPSS je príkaz nasledovný:
- ANALYZE/ COMPARE MEANS/ PAIRED-SAMPLES T-TEST. Po otvorení okna je potrebné do PAIRED VARIABLES postupne preniesť premennú prvého (VARIABLE 1) a premennú druhého merania (VARIABLE 2) 27. Odklikneme už len /OK.
Vo výstupe z SPSS sú tri tabuľky. V prvej môžeme vidieť deskriptívne parametre (priemer, ŠO, interval spoľahlivosti,…), v druhej je výsledok korelácie premennej prvého a druhého merania. Ide o medzikrok testovania, väčšinou ide o silnú či veľmi silnú koreláciu (r > 0,5), výnimočne sa stane, že korelácia nie je významná. V tretej tabuľke je výsledok samotného párového t-testu (tento je relevantný pre samotné porovnanie meraní).
Interpretácia výsledku testovania:Predpoklad sme overovali použitím t-testu pre dva závislé výbery, ktorého výsledky prezentuje tabuľka (Tabuľka 15). Lineárna závislosť premenných prvého a druhého merania dosahuje r = 0,625, pri Sig. < 0,001. Výsledok t-testu poukazuje na významný rozdiel medzi meraniami (t = - 3,303, Sig. < 0,01). Hypotézu H7 (a tiež dvojsmernú H7a) prijímame. Medzi meraniami pred a po aplikácii interakčného učenia došlo k štatisticky významnému rozdielu v sebadôvere. (Uvedená interpretácia postačuje pre dvojsmerne formulované hypotézy.)
Ak je hypotéza jednosmerná, po zistení významného rozdielu (tzn. Sig. < 0,05. Ak by bola Sig. > 0,05, hypotézu priamo zamietneme) sledujeme ďalej aj hodnotu priemerov a priemerného rozdielu s cieľom identifikovať, v ktorom meraní sú hodnoty vyššie či nižšie.
V prvej časti tabuľky (Tabuľka 15) sú uvedené priemerné hodnoty pre prvé merania (19,0) a druhé meranie (21,9) sebadôvery, s rozdielom -2,87. Z uvedeného vyplýva, že pri druhom meraní sebadôvery po aplikácii interakčného učenia sú jej hodnoty vyššie (došlo k zlepšeniu sebadôvery). Hypotézu H7b prijímame.
Tabuľka 15 Výsledky testovania H7 (H7a, H7b): T-test pre dva závislé výbery
| Priemer | N | ŠO | Korelácia (r) | Sig. | |
| Sebadôvera PRED | 19,0 | 30 | 5,4 | ,625 | ,000 |
| Sebadôvera PO | 21,9 | 30 | 5,6 | ||
| Párové rozdiely | Párový t-test | ||||
| Sebadôvera PRED- Sebadôvera PO | Priemer rozdielov | ŠO rozdielu | t | df | Sig. |
| -2,87 | 4,75 | -3,303 | 29 | ,003 | |
Graf, ktorý by sme mohli v tomto prípade použiť na zobrazenie rozdielov medzi
meraniami je error bar (Graf 13) alebo boxplot28.
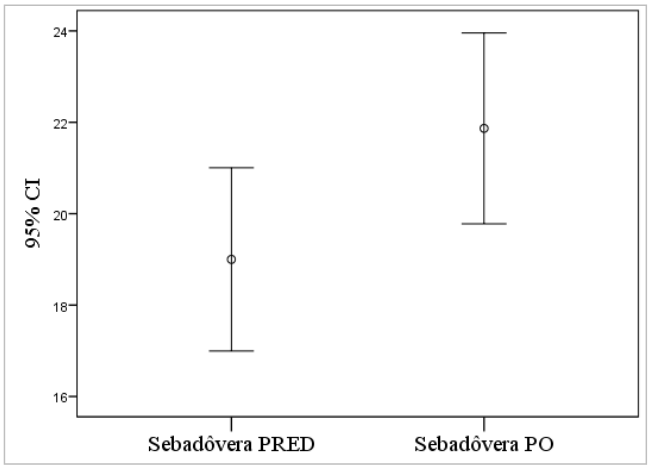
Graf 13 Error Bar znázorňujúci premenné Sebadôvera PRED a Sebadôvera PO
B. NEPARAMETRICKÉ TESTOVANIE
Neparametrické komparačné testy, ako sme už uviedli vyššie, pracujú na princípe porovnávania poradí, teda nie reálnych stredných hodnôt, ale transformovaných. Po zoradení respondentov porovnávaných skupín do poradia, vypočítaním priemerných poradí pre každú skupinu sa štatisticky testujú rozdiely medzi priemernými poradiami. Pri závislých výberoch však nie je súbor rozdelený na skupiny, ale ide o dve merania v tom istom súbore. Preto nie je možné použiť rovnaký princíp. Neparametrické testy preto pracujú na princípe tzv. „ZNAMIENKA“, znamienko označuje kladný alebo záporný rozdiel určený pre každého jedného respondenta, teda, či u neho pri druhom meraní došlo k zníženiu (-) alebo k zvýšeniu (+) hodnoty premennej. Test, ktorý pracuje iba na báze znamienok sa volá ZNAMIENKOVÝ TEST (Sign Test) a používa sa najčastejšie pri testovaní zmien v javoch, ktoré sú škálované ordinálne, pričom hodnoty dosahujú malé spektrum (napr. v rozsahu 0 – 4). Presnejším neparametrickým testom, ktorý znamienkový princíp dopĺňa aj o výpočet a porovnanie priemerných poradí, je WILCOXONOV ZNAMIENKOVO- PORADOVÝ TEST. Uvedený test akoby rozdelí súbor podľa + a – znamienok na dve skupiny, pre každú vypočíta priemerné poradia, ktoré reprezentujú aj veľkosť rozdielov, a teda nie iba smer (+ alebo -) ako znamienkový test, a príslušnú štatistickú významnosť rozdielov v priemerných poradiach. Wilcoxonov test je teda vhodnejší, pokiaľ dosahuje ordinálna premenná väčšie spektrum hodnôt (0 – 8, 0 – 10), alebo ak počíta rozdiel v meraniach kardinálnych, ale nie normálne distribuovaných premenných. Výsledky z SPSS potom obsahujú tabuľku s početnosťou pozitívnych (Positive Ranks), negatívnych (Negative Ranks) a zhodných poradí (Ties), priemerné poradia pre pozitívne a negatívne poradia (zmeny) medzi meraniami. Nasleduje tabuľka s výsledkom Wilcoxonovho testu s hodnotou Z a príslušnou Sig., teda štatistickou významnosťou rozdielu medzi pozitívnymi a negatívnymi poradiami.
Príklad 8:
H8 (výskumná dvojsmerná): Predpokladáme, že počas fyzioterapie dôjde k zmene prežívania bolesti v zoperovanej končatine.
Ekvivalenty:
H8a (dvojsmerná): Predpokladáme, že medzi meraním bolesti VAS škálou pred fyzioterapiou a meraním bolesti VAS škálou po fyzioterapii bude významný rozdiel.
H8b (jednosmerná): Predpokladáme, že v priebehu fyzioterapie dôjde k významnému zníženiu bolesti meranej VAS škálou..
Zopakujeme si, kedy volíme neparametrický test na overenie komparačnej hypotézy: ak ide o ordinálne premenné alebo ak kardinálne premenné nespĺňajú kritérium normálneho rozdelenia (zistíme testom normality), prípadne, ak je súbor, v rámci ktorého sa porovnávajú merania malý ( n < 30). V uvedenom prípade ide o ordinálnu premennú Vizuálnej škály bolesti VAS, ktorá dosahuje hodnoty 0 – 10 bodov, kde 0 znamená „žiadna bolesť“ a 10 „najhoršia bolesť, akú si viete predstaviť“. Na testovanie rozdielov medzi meraniami pred a po fyzioterapii použijeme neparametrický WILCOXONOV ZNAMIENKOVO-PORADOVÝ TEST (Wilcoxon Signed Ranks Test).
Postup v SPSS je nasledovný:
- ANALYZE/ NONPARAMETRIC TESTS/ LEGACY DIALOGS/ 2 RELATED SAMPLES; po otvorení okna presunieme do TEST PAIRS premennú prvého merania (VARIABLE 1, v tomto príklade VAS 1) a následne premennú druhého merania (VARIABLE 2, tu je to premenná VAS 2)29. V okne máme možnosť zaškrtnúť typ testu. Zvolíme WILCOXON a tiež môžeme v možnosti /OPTION zaškrtnúť DESCRIPTIVE, pri ordinálnych premenných je vhodné označiť aj QUARTILES (vo výsledkoch budeme vidieť deskriptívne parametre), klikneme na /OK.
Vo výstupovom okne uvidíme tri tabuľky. Prvá obsahuje deskriptívne parametre jednotlivých meraní premennej. Druhá uvádza výsledky výpočtov znamienok a poradí, ktoré sú podkladom pre testovanie. V tretej tabuľke je výsledok samotného testu s príslušnou hodnotou štatistickej významnosti Sig. Tabuľky je možné integrovať do jednej, ako je to možné vidieť nižšie ( Tabuľka 16).
Interpretácia výsledku:
Predpoklad sme overovali použitím Wilcoxonovho znamienkovo-poradového testu pre 3 a viac závislých výberov, ktorého výsledky prezentuje tabuľka (Tabuľka 16). Výsledok testu poukazuje na významný rozdiel medzi meraniami ( Z = – 8,868, Sig. < 0,001). Hypotézu H8 (a tiež dvojsmernú H8a) prijímame. Medzi meraniami pred a po fyzioterapii došlo k štatisticky významnému rozdielu v bolesti (na škála VAS). (Uvedená interpretácia postačuje pre dvojsmerne formulované hypotézy.)
Ak je hypotéza jednosmerná, po zistení významného rozdielu (tzn. Sig. < 0,05. Ak by bola Sig. > 0,05, hypotézu priamo zamietneme) sledujeme ďalej počet negatívnych a pozitívnych poradí a tiež hodnoty priemerných poradí s cieľom identifikovať, v ktorom meraní sú hodnoty vyššie či nižšie.
V prvej časti tabuľky (Tabuľka 16) sú uvedené deskriptívne hodnoty pre prvé merania (M = 5,6; Med = 6) a druhé meranie (M = 1,3; Med = 1) bolesti. V dolnej časti tabuľky môžeme vidieť, že v 97 prípadoch bola hodnota v druhom meraní nižšie ako v prvom (označenie „a“) v dvoch prípadoch vyššia (označenie b) a v jednom prípade rovnaká. Priemerné poradie pri negatívnych poradiach bolo 51, pri pozitívnych poradiach 1,5. Z uvedeného vyplýva, že pri druhom meraní bolesti po fyzioterapii sú jej hodnoty štatisticky významne nižšie. Hypotézu H8b prijímame.
Tabuľka 16 Výsledky testovania H8 (H8a, H8b): Wilcoxonov znamienkovo-poradový test
| N | Priemer | Štd.odch. | Min. | Max. | 1. kvartil | Medián | 3. kvartil | |
| VAS 1 | 100 | 5,6 | 1,1 | 3 | 7 | 5 | 6 | 6 |
| VAS 2 | 100 | 1,3 | 0,8 | 0 | 4 | 1 | 1 | 2 |
| Poradia | N | Priemerné poradie | Wilcoxonov test | ||
| VAS 2 – VAS 1 | Negatívne | 97a | 51 | Z | -8,868 |
| Pozitívne | 2b | 1,5 | Sig. | ,000 | |
| Zhodné | 1c | ||||
| Spolu | 100 | ||||
Výsledky neparametrického porovnanie viacerých meraní premennej je vhodné graficky znázorniť prostredníctvom jednoduchého boxplotu pre samostatné premenné30, ako je to v grafe (Graf 14).
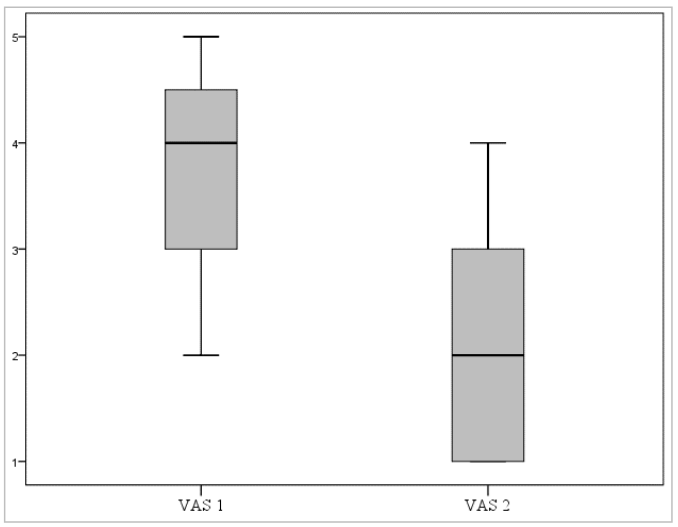
Graf 14 Boxplot znázorňujúci premenné VAS 1 a VAS 2
10.2 Komparácia 3 a viac meraní závislých výberov
V prípade, ak je jedna premenná meraná v jednom súbore viac ako dvakrát, na testovanie zmien medzi meraniami sa používajú špecifické testy. Ide o merania jednej premennej u rovnakých participantov, medzi ktorými je určitý časový interval. Rovnako ako v predchádzajúce podkapitole môžeme povedať, že k takýmto meraniam dochádza v experimentálnych (či kváziexperimentálnych) alebo v longitudinálnych štúdiách. Podľa normálneho rozdelenia premenných, pričom každá premenná každého merania je samostatnou premennou, a typu premenných (K, O) potom volíme parametrické a neparametrické testovanie.
Vzhľadom na to, že v študentských prácach len zriedka dochádza k uvedenému typu výskumov s 3 a viac meraniami, v podkapitole iba uvedieme, o aké testy ide, príkaz v SPSS a stručný popis údajov, ktoré nájdeme vo výstupových tabuľkách, teda bez uvedenia príkladov.
A. PARAMETRICKÉ TESTOVANIE
Pokiaľ je kardinálna premenná vo všetkých meraniach (3 a viac) normálne rozdelená, alebo pokiaľ ide o veľké súbory, môžeme pre testovanie rozdielov medzi meraniami použiť REPEATED MEASURES ANOVA (analýzu rozptylu pre opakované merania). Test pracuje na báze porovnania priemerov a v SPSS ho nájdeme
postupom:
- ANALYZE/ GENERAL LINEAR MODEL/ REPEATED MEASURES: najskôr sa otvorí okno DEFINED FACTOR(S), kde do prvého riadku môžeme prepísať názov pôsobiaceho faktora WITHIN-SUBJECT FACTOR NAME. Pri opakovaných meraniach ide o časový faktor, preto ho môžeme nazvať, napríklad, „Time“, a do NUMBER OF LEVELS napíšeme počet meraní a klikneme na /ADD (zadanie sa objaví napravo v okienku) a /DEFINE. V nasledujúcom testovom okne presunieme do pravého horného WITHIN-SUBJECT VARIABLES (factor 1) postupne premenné jednotlivých meraní. Pod /OPTIONS (samostatné okno) presunieme faktor „Time“ doprava a nižšie zaškrtneme DESCRIPTIVE STATISTICS a ESTIMATES OF EFFECT SIZE. Odklikneme /CONTINUE a /OK.
Vo výsledkoch hľadáme tabuľku Tests of Within-subjects Effects a konkrétne „Greenhouse-Geisser“ riadok, kde Sig. vypovedá o významnosti rozdielov medzi meraniami (rozdiel je významný pokiaľ Sig. < 0,05), Partial Eta Squared o veľkosti efektu. Do výsledkov sa uvádza tiež F hodnota. Konkrétne priemery (a štandardné odchýlky) pre merania nájdeme v tabuľke Descriptive Statistics, podľa ktorých interpretujeme smerovanie rozdielov.
B. NEPARAMETRICKÉ TESTOVANIE
Neparametrický FRIEDMAN`S test for Several Related Samples použijeme vtedy, pokiaľ ide pri meraniach o ordinálne premenné, alebo pokiaľ kardinálne premenné v každom meraní nemajú normálnu distribúciu, obzvlášť v malých súboroch. Test pracuje na princípe porovnania priemerných poradí (Mean Ranks).
Postup:
- ANALYZE/ NONPARAMETRIC TESTS/ LEGACY DIALOGS/ K RELATED SAMPLES: po otvorení okna presunieme postupne premennú každého merania (3 alebo viac) do TEST VARIABLES a v TEST TYPE ponecháme zaškrtnutý FRIEDMAN. Otvoríme príkaz /STATISTICS a zaškrtneme DESCRIPTIVE. Odklikneme /CONTINUE a /OK.
Vo výstupných tabuľkách nájdeme ako prvú tabuľku s deskripciou (ak sme zaškrtli Descriptive), potom tabuľku s priemernými poradiami, ako tretia je tabuľka s výsledkom testu a hodnotou štatistickej významnosti Sig., Do výsledkov uvádzame tiež hodnotu Chí-kvadrátu (Chí-square). Rozdiely považujeme za významné, pokiaľ Sig. < 0,05, v tom prípade smerovanie rozdielov medzi meraniami interpretujeme podľa priemerných poradí (Mean Ranks, nižšie, vyššie, najvyššie hodnoty).
10.3 Alternatívne možnosti použitia párového testu
V niektorých prípadoch nájdeme použitie párových testov v štúdiách aj vtedy, ak sa porovnávajú rôzne premenné v tom istom čase. Porovnávané premenné ale musia byť merané jedným meracím nástrojom, kde je rovnakými položkami alebo na rovnakom rozsahu hodnôt zisťovaný paralelný jav. Napríklad Dotazník na zisťovanie spôsobu výchovy v rodine (Čáp a Boschek, 1994) meria 4 komponenty výchovy u matky a rovnakým spôsobom (rovnakými položkami) u otca. Je teda možné porovnať tieto dve premenné a zistiť, či je vyšší kladný komponent u otca alebo u matky, alebo vôbec, či sa štatisticky líšia.
Iným príkladom je napr. zisťovanie, či existujú rozdiely medzi skóre v copingovej stratégii Hľadanie sociálnej opory a v stratégii Riešenie problému (prípadne inej) u nejakej skupiny (napr. u slobodných matiek). Je to možné iba vtedy, pokiaľ je možné dosiahnuť v týchto škálach/stratégiách rovnaké skóre (rovnaký počet položiek) a priemerné hodnoty v populácii sú v oboch stratégiách nerozdielne.
Použitie je tiež možné, pokiaľ jeden merací nástroj meria premennú u viacerých ľudí v malej sociálnej skupine. Porovnáme napríklad vnímanie kvality komunikácie vo vzťahu medzi partnermi tak, že odmeriame dotazníkom premennú u ženy a rovnakým u muža, pričom v databáze máme hodnoty v jednom riadku (riadok tak reprezentuje jednotku = pár). Podobne sa dá párové testovanie použiť napr. na porovnanie výchovného štýlu (ktorý uplatňovali u svojich detí) matky a starej mamy, ak chceme zistiť, či existuje rozdiel v miere ambivalencie vo výchove medzi rodičom a starým rodičom. Rovnako vtedy riadok v databáze reprezentuje rodinnú jednotku (a nie teda jednotlivca, ako je to bežne).
ÚLOHY
- Sformulujte dvojsmernú a potom jednosmernú hypotézu o zmene v klíme na pracovisku po tom, ako kolektív absolvuje spoločný regeneračný program v horách.
- Zamyslite sa, o akú premennú ide a skúste ju operacionalizovať (vymyslite si, ako a koľkokrát by sa mohla merať).
- Aké parametre by ste museli zohľadniť pri výbere testu? Medzi akými štatistickými testami by ste sa rozhodovali?
- Sformulujte akúkoľvek jednosmernú hypotézu o rozdiele medzi viacerými (dvomi či tromi) meraniami premennej (K, O) s použitím cvičnej (či vlastnej) databázy.
- Zohľadnite potrebné parametre (normalita, štandardnosť testu, veľkosť vzorky) a zvoľte typ štatistické testu.
- Hypotézu otestujte (v SPSS), výsledky spracujte do tabuľky a interpretujte.
- Výsledok zobrazte príslušným grafom.
- Uvažujte ešte o iných prípadoch rôznych premenných (nie viacerých meraní premennej), ktoré by boli merané takým spôsobom (nástrojom), aby ich bolo možné porovnať párovým testom.

