ŠTATISTIKA PRAKTICKY (NIELEN) V ZÁVEREČNÝCH PRÁCACH
11.KORELÁCIA MEDZI DVOMA KVANTITATÍVNYMI PREMENNÝMI
Súvislosti v zmysle lineárnych vzťahov (priama/nepriama úmernosť) medzi dvoma kvantitatívnymi (kardinálnymi či ordinálnymi) premennými môžu byť testované prostredníctvom korelačného koeficientu.
Diferencujeme medzi parametrickou verziou – PEARSONOV KOEFICIENT SÚČINOVEJ KORELÁCIE a neparametrickou verziou – SPEARMANOV KOEFICIENT PORADOVEJ KORELÁCIE. Pearsonov koeficient počíta lineárny vzťah medzi reálnymi hodnotami premenných v databáze, pričom je podmienkou, aby išlo o kardinálne a (obe) normálne rozdelené premenné31. Spearmanov
koeficient počíta lineárny vzťah medzi poradiami, ktoré vznikli na základe usporiadania respondentov podľa ich reálnych hodnôt, každému respondentovi sú teda priradené 2 poradia, jedno pre prvú premennú, druhé pre druhú premennú 32. Koeficient je počítaný medzi poradiami, teda nie medzi reálnymi nameranými hodnotami. Preto je táto neparametrická verzia vhodná na testovanie vzťahov, pokiaľ sú premenné ordinálne, alebo kardinálne nevyhovujúce pre parametrické testovanie (malé súbory, nie normálne distribuované). Výsledky štatistického testovania obsahujú výpočet korelačného koeficientu (r alebo ρ33) a príslušnú štatistickú významnosť vzťahu (Sig.). Interpretácia sa opiera o:
- zhodnotenie štatistickej významnosti Sig.:
- pokiaľ táto je menšia ako stanovená hladina α (štandardne 0,05), vzťah
(lineárny) je významný (Sig. < 0,05),- interpretuje sa ďalej SMEROVANIE VZŤAHU, teda či je hodnota korelačného koeficientu r (ρ) kladná alebo záporná. Kladná svedčí o priamej úmernosti, záporná o nepriamej úmernosti;
- interpretuje sa tiež SILA VZŤAHU, podľa samotnej hodnoty
korelačného koeficientu r (ρ), a to v psychológii štandardne
nasledovným spôsobom (Cohen, 1993), platí pre kladné i záporné hodnoty:0 až 0,1 – žiadny, triviálny vzťah; 0,1 až 0,3 – slabý vzťah; 0,3 až 0,5 – stredne silný vzťah; 0,5 až 0,7 – silný vzťah; 0,7 až 0,9 – veľmi silný vzťah; 0,9 až 1 – dokonalý vzťah, premenné sú totožné
- pokiaľ je Sig. > 0,05, vzťah nie je významný, na výskumnú otázku (o existencii vzťahu medzi premennými) odpovedáme záporne, alebo zamietame hypotézu o vzťahu medzi premennými
- pokiaľ táto je menšia ako stanovená hladina α (štandardne 0,05), vzťah
Príklad 8 – kardinálne premenné:
H8: Predpokladáme, že existuje (lineárny) vzťah medzi Pozitívnym vzťahom
ku škole a Podporou od učiteľa (dvojsmerná).
Ekvivalenty:
H8a: Predpokladáme, že Pozitívny vzťah ku škole lineárne súvisí s Podporou od učiteľa (dvojsmerná).
H8b: Predpokladáme, že medzi Pozitívnym vzťahom ku škole a Podporou od učiteľa existuje kladný korelačný vzťah (priamoúmerný) (jednosmerná).
H8c: Predpokladáme, že čím je podpora od učiteľa u žiaka vyššia, tým má žiak pozitívnejší vzťah ku škole (jednosmerná).
Testovanie v SPSS realizujeme cez zadanie:
- ANALYZE/ CORRELATE/ BIVARIATE, po ktorom bude otvorené dialógové
okno na zadanie premenných (VARIABLES). Tu vložíme z ľavého panelu príslušné premenné, medzi ktorými zisťujeme vzťah 34, nezáleží na poradí (v tomto prípade Podpora od učiteľa a Pozitívny vzťah ku škole). Ďalej je potrebné zaškrtnúť príslušný CORRELATION COEFFICIENTS – podľa vyššie
uvedeného, najčastejšie rozhodujeme medzi PEARSONOVÝM a SPEARMANOVÝM.
V tomto prípade môžeme zvoliť (aj) parametrický koeficient, keďže premenné sú kardinálne, vzorka je veľmi veľká, čo znamená, že i keď by premenné neboli normálne rozložené, výsledky skreslené nebudú (nebude interpretačný rozdiel medzi výsledkom neparametrického a parametrického testu), čo môžeme vidieť vo
výsledkoch a interpretácii. Viac k voľbe testu nájdete v kapitole 7.2. Výsledky generujú jedinú tabuľku pre každý typ koeficientu (ak sme zadali oba typy, tak sú
tabuľky dve), tento typ tabuľky nazývame KORELAČNÁ MATICA.
Interpretácia výsledku:
Hypotéza H8 bola testovaná použitím výpočtu Spearmanovho koeficientu poradovej korelácie, ktorého výsledok uvádzame v tabuľke (Tabuľka 17). Na základe zistenej štatistickej významnosti Sig. < 0,001 považujeme korelačný vzťah medzi premennými Podpora od učiteľa a Pozitívny vzťah ku škole za významný. Hypotézu H8 (rovnako H8a – čiže dvojsmerné hypotézy) prijímame. Podpora učiteľa lineárne súvisí s pozitívnym vzťahom ku škole. (Uvedená interpretácia postačuje, pokiaľ je hypotéza dvojsmerná)
Pokiaľ je hypotéza jednosmerná a bol zistený významný vzťah (čiže Sig. < 0,05. Pokiaľ je Sig. vyššia než 0,05, vzťah významný nie je, hypotézu rovno zamietame), pokračujeme interpretáciou hodnoty korelačného koeficientu:
Hodnota Spearmanovho/Pearsonovho korelačného koeficientu je ρ = 0,443/ r = 0,455. Ide o pozitívny (kladný), stredne silný vzťah, čo znamená že medzi premennými je priama úmernosť. Čím je podpora od učiteľa vyššia, tým je vzťah žiaka ku škole pozitívnejší. So vzrastajúcim skóre jednej premennej vzrastá skóre druhej premennej. Hypotézu H8b (a rovnako H8c) prijímame.
Tabuľka 17 Výsledky testovania H8: Spearmanov koeficient poradovej korelácie (ρ) a Pearsonov koeficient súčinovej korelácie (r) vzťahu medzi Podporou od učiteľa a Pozitívnym vzťahom ku škole
| Podpora od učiteľa | ||
| Pozitívny vzťah ku škole | Spearmanovo ρ | ,443 |
| Sig. | ,000 | |
| N | 2410 | |
| Pozitívny vzťah ku škole | Pearsonovo r | ,455 |
| Sig. | ,000 | |
| N | 2410 |
Lineárne vzťahy medzi kardinálnymi premennými je možné zobraziť graficky grafom scatterom (Graf 15), ktorý je možné doplniť tzv. „FIT LINE at total“ priamkou – táto uhlom svojho naklonenia od osi x znázorňuje silu, orientáciou (zľava dolu smerom doprava hore, alebo opačne) aj polaritu lineárneho vzťahu.
Príklady 9 a 10 – ordinálne premenné:
H9: Predpokladáme, že školský prospech súvisí s počtom dobrých priateľov (dvojsmerná).
H10: Predpokladáme, že jednotlivec má tým lepší prospech, čím viac detí s ním žije v domácnosti (jednosmerná).
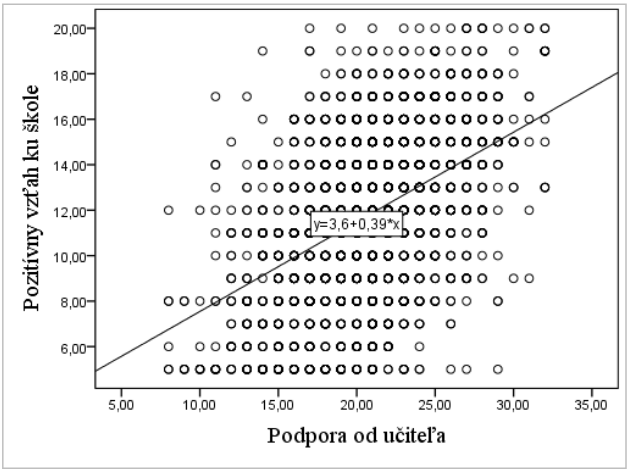
Graf 15 Scatter graf zobrazujúci lineárnu závislosť medzi premennými Pozitívny vzťah ku škole a Podpora od učiteľa
Operacionalizujeme premenné35, aby sme pochopili ich ordinálny charakter:
Školský prospech dosahuje hodnoty od 1 – 8, pričom 1 znamená, že žiak má väčšinou jednotky, 2 – má väčšinou jednotky a dvojky….., 7 – má väčšinou štvorky a 8 – väčšinou štvorky a päťky. Hodnota teda nie je exaktne matematicky určená a ide
jednoznačne o ordinálnu škálu, v dotazníku reprezentovanú slovnými odstupňovanými výpoveďami.
Počet dobrých priateľov nadobúda hodnoty: 1 – nemám žiadnych, 2 – jedného, 3-
dvoch…, 5- päť či viac. Ide teda rovnako o ordinálnu premennú.
Počet detí v domácnosti je vyjadrený v dotazníku číslami, pričom najvyššiu hodnotu má odpoveď: 6 či viac detí. Ak by tu boli reálne čísla, neobmedzené poslednou
hodnotou, premenná by bola kardinálna. Ak však je odpovedanie obmedzené do „6
a viac“, ide o ordinálnu premennú.
Na vyhodnotenie oboch hypotéz je použitý Spearmanov korelačný koeficient,
výsledky k obom hypotézam je možné uviesť v jedinej tabuľke (Tabuľka 18).
Hypotézu H9 sme overovali Spearmanovým koeficientom poradovej korelácie s výsledkom ρ = 0,075 a Sig. < 0,001. Vzhľadom k hodnote významnosti je možné zistený vzťah považovať za štatisticky významný, avšak môžeme vidieť, že jeho hodnota je menšia ako 0,1, čo štatisticky interpretujeme ako triviálny (banálny) vzťah.
Môžeme povedať, že s viac ako 99,9% istotou (o tom vypovedá hodnota Sig.) je medzi premennými triviálny vzťah. Formálne alternatívnu nenulovú hypotézu prijímame (štatistická interpretácia), ale vecne (tzn. v diskusii) vzťah neinterpretujeme36!
Hypotézu H10 sme overovali rovnakým testom (Spearmanov korelačný koeficient), s výsledkom ρ = -0,115 a Sig. < 0,001. Zistený vzťah je štatisticky významný.
Pretože ide o jednosmernú hypotézu a hodnota koeficientu je v interpretovateľnom intervale 0,1 – 0,3, čo svedčí pre slabý vzťah, musíme pre prijatie hypotézy zvážiť aj smerovanie (polaritu) vzťahu. Ide o záporný koeficient, ktorý hovorí o tom, že čím je jedna premenná vyššia, tým je druhá premenná nižšia. Vždy sa musíme dôkladne zamyslieť, čo znamenajú nízke a vysoké hodnoty premenných. V tomto prípade interpretujeme ďalej:
Medzi premennými je záporný slabý vzťah. Čím dosahuje prospech nižšie hodnoty (je lepší), tým je počet detí v domácnosti vyšší. Hypotézu H10 prijímame.
Tabuľka 18 Výsledky testovania H9 a H10: Spearmanov koeficient poradovej korelácie
| Počet dobrých priateľov | Počet detí v domácnosti | ||
Prospech v škole
(1 = najlepší,… 8 = najhorší) | Spearmanovo ρ | 0,075 | -,115 |
| Sig. | ,000 | ,000 | |
| N | 2410 | 2410 |
V prípade zisťovania vzťahov medzi ordinálnymi premennými nie je vhodný graf scatter. Odporúčame pre zobrazenie vytvoriť kontingenčný graf v Exceli.
ÚLOHY
- Sformulujte dvojsmernú a potom jednosmernú hypotézu o vzťahu medzi inteligenciou a hodnotením z predmetu o štatistike
- Zamyslite sa, o aké premenné ide a premenné skúste operacionalizovať (vymyslite si, ako by ste ich mohli merať).
- Aký korelačný test by ste zvolili? Rozhodnutie odôvodnite.
- Sformulujte akúkoľvek jednosmernú hypotézu o vzťahu dvoch kvantitatívnych (O, K) premenných s použitím cvičnej (či vlastnej) databázy.
- Zohľadnite potrebné parametre (normalita, štandardnosť testu, veľkosť vzorky) a zvoľte typ štatistické testu.
- Hypotézu otestujte (v SPSS), výsledky spracujte do tabuľky a interpretujte.
- Výsledok zobrazte príslušným grafom

