ŠTATISTIKA PRAKTICKY (NIELEN) V ZÁVEREČNÝCH PRÁCACH
12.LINEÁRNA REGRESNÁ ANALÝZA
Ako sme zistili v predchádzajúcej kapitole, unikátny vzťah medzi dvomi premennými je možné vyjadriť prostredníctvom korelačného koeficientu (resp. taktiež silu a smer tohto vzťahu). Medzi vnímanou mierou podpory od učiteľa a
pozitívnym vzťahom ku škole bol kladný, stredne silný vzťah. Čím bola podpora od učiteľa vyššia, tým bol vzťah žiaka ku škole pozitívnejší. Ak zistíme prostredníctvom korelačného koeficientu, že medzi dvomi premennými existuje súvislosť, dokážeme vysloviť taktiež predikciu.
Korelačný koeficient vyjadruje, že sa hodnoty jednej premennej menia súčasne pri zmenách hodnôt druhej premennej, avšak regresná analýza dokáže odpovedať na otázku (1) aký veľký efekt má nezávislá premenná na závislú premennú a zároveň (2) akú hodnotu bude mať závislá premenná za určitej hodnoty nezávislej premennej. Resp. na základe známych hodnôt jednej premennej je možné predpovedať hodnoty druhej premennej.
Predikcia je však spoľahlivá jedine v takom prípade, že zistíme súvislosť medzi
dvoma (alebo viacerými) premennými. Miera spoľahlivosti predikcie na základe sily
vzťahu medzi premennými teda môže kolísať od irelevantnej až po veľmi dobrú. Možnými príkladmi takýchto predikcií sú: Predikuje miera vnímaného šťastia kvalitu života človeka? Ako IQ predikuje hodnotenie zamestnancov ako kompetentných? Ako IQ, doba štúdia, socioekonomický status a motivácia predikujú akademický výkon študentov? Ako úroveň stresu, zvládanie stresu a sociálna podpora ovplyvňujú psychické zdravie jedincov? Je možné prostredníctvom spokojnosti s pracovnými podmienkami, platom, pracovnou istotou a interpersonálnymi vzťahmi predikovať celkovú pracovnú spokojnosť
zamestnancov? Do akej miery osobnostné črty (extroverzia, neurotizmus, svedomitosť) predikujú rizikové správanie?
Už z uvedených príkladov je možné vidieť, že regresnú analýzu môžeme uskutočniť pre dvojicu premenných a taktiež pre viacero premenných, pričom pre druhú situáciu platí, že uvádzame niekoľko prediktorov (nezávislých premenných) a jednu závislú premennú. Na základe počtu premenných rozlišujeme JEDNODUCHÚ REGRESNÚ ANALÝZU a VIACNÁSOBNÚ REGRESNÚ ANALÝZU.
Prediktor (nezávislá premenná) je taká premenná, ktorú využijeme na predpovedanie
závislej premennej a cieľom každej regresnej analýzy je predikovanie (resp.
predpovedanie) hodnôt závislej premennej (niekedy sa závislá premenná nazýva tiež
výsledná, predikovaná alebo kriteriálna premenná). Pokiaľ hovoríme o závislých a
nezávislých premenných, naznačuje to kauzálny (príčinno-následný) vzťah, dôležité
je však podotknúť, že kauzálne vzťahy zisťujeme prostredníctvom realizovania
experimentálnych výskumov! Lineárnu regresnú analýzu využívame taktiež v korelačných dizajnoch, čo znamená, že viacero premenných je nameraných súčasne a nie je možné s nimi manipulovať (tak ako by to bolo možné v experimentálnom výskume). Z uvedeného vyplýva, že o kauzálnych vzťahoch v takomto prípade iba usudzujeme, ale nevieme ich dokázať. Dokážeme predpovedať napr. do akej miery osobnostné črty predikujú rizikové správanie, ale nedokážeme prostredníctvom regresnej analýzy overiť, či je tento vzťah kauzálny. V zásade hovoríme o časovej následnosti, v uvedenom príklade sú osobnostné črty relatívne stabilné a preto časovo predchádzajú rizikovému správaniu, na základe poznania spojitosti medzi osobnostnými črtami a rizikovým správaním ho dokážeme predpovedať. V ďalšom texte budeme využívať pojem prediktor (pre nezávislú premennú) a pojem závislá premenná (nakoľko danú premennú predpovedáme).
Výsledky štatistického testovania obsahujú výpočet:
- Regresný koeficient (B alebo β) – smernica regresnej priamky. Rozlišujeme dva regresné koeficienty – B je neštandardizovaný regresný koeficient, je vyjadrený v jednotkách, v ktorých bol nameraný a β je štandardizovaný regresný koeficient, je štandardizovaný tak aby dosahoval hodnotu -1 až 1.
Jeho hodnotu interpretujeme takto:
- kladná hodnota – regresná priamka je stúpajúca
- záporná hodnota – regresná priamka je klesajúca
- nulová hodnota – regresná priamka je rovnobežná s osou X.
- Regresná konštanta (a, alebo B0) – vyjadruje odhadovanú hodnotu závislej premennej (y) ak sa hodnota prediktoru (x) rovná nule (význam je v niektorých prípadoch psychologického výskumu iba formálny).
- Štatistická významnosť – signifikancia – interpretácia je štandardná ako pri iných testoch štatistickej významnosti.
12.1 Jednoduchá lineárna regresná analýza
Jednoduchá lineárna regresná analýza predstavuje základný model pre rôzne predikcie. Podobne ako bivariačná korelačná analýza, skúma vzťah dvoch premenných. Avšak jej cieľom je nie len popísať silu a smer vzťahu medzi premennými ale taktiež predpovedať hodnoty závislej premennej
Aké sú podmienky lineárnej regresnej analýzy?- Vzťah medzi premennými musí byť lineárny – Nakoľko lineárna regresná analýza vychádza z korelačnej analýzy, jej základnou podmienkou je lineárny vzťah medzi dvomi premennými. Lineárny vzťah znamená, že je možné vyjadriť ho prostredníctvom priamky, resp. danú podmienku budeme testovať graficky vždy pred realizáciou regresnej analýzy.
- Závislá premenná je meraná na intervalovej úrovni a nezávislá premenná je taktiež intervalová, prípadne dichotomická.
- Premenné sú normálne rozložené (samozrejme, výnimku predstavuje dichotomická premenná). Danú podmienku testujeme pri menších výskumných vzorkách (N < 100) nakoľko vďaka centrálnej limitnej vete vieme, že nenormálne rozloženie vo veľkých výskumných vzorkách zásadne neovplyvňuje výsledky.
Príklad 11 – kardinálne premenné:
H11: Predpokladáme, že optimizmus predikuje životnú spokojnosť .
Pred samotnou realizáciou výpočtu overíme podmienky lineárnej regresnej analýzy. Obidve premenné sú merané na intervalovej úrovni (jedná sa o celkové skóre dvoch dotazníkov s veľkým rozptylom), nakoľko je výskumná vzorka tvorená veľkým počtom participantov (N = 434), nie je potrebné overovať prítomnosť normálneho rozloženia. Overíme prvú podmienku realizácie, ktorou je lineárny vzťah medzi skúmanými premennými
Testovanie linearity v SPSS realizujeme cez zadanie:- GRAPHS/ CHART BUILDER, po ktorom bude otvorené dialógové okno pre výber grafu. V časti GALLERY je možné zvoliť vhodný typ grafu, v tomto prípade SCATTER PLOT (nakoľko pre tento typ grafu bude možné zobraziť regresnú priamku). Vľavo hore nájdeme hľadané premenné optimizmus a životnú spokojnosť. Prediktor (v tomto prípade optimizmus) presunieme na os X a závislú premennú (životná spokojnosť) na os Y. Stlačíme OK.
- Na zobrazený graf klikneme dvakrát, čím sa otvorí v samostatnom okne a vyberieme možnosť FIT LINE AT TOTAL (druhý riadok v ponuke možností), týmto úkonom sa vytvorí regresná priamka. Výsledkom tohto zadania je Graf 16, na základe ktorého môžeme pozorovať, že tvar vzťahu medzi životnou spokojnosťou a optimizmom je možné považovať za približne lineárny. Na základe tohto výsledku môžeme použiť lineárnu regresnú analýzu.
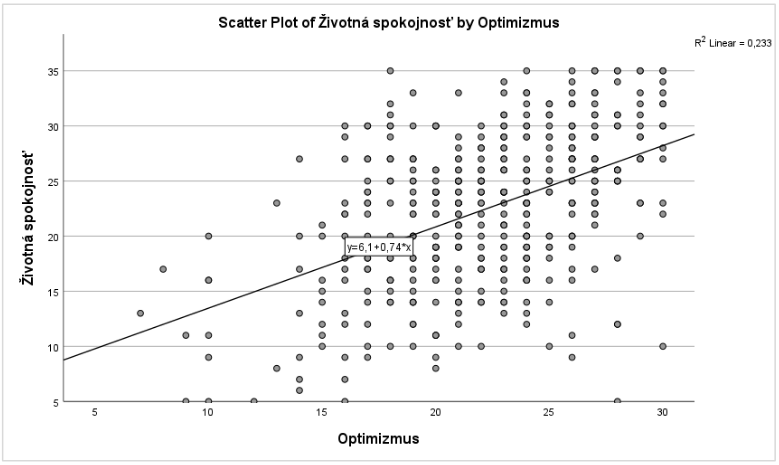
Graf 16 Bodový graf zobrazujúci lineárny vzťah medzi premennými optimizmus a životná spokojnosť
Testovanie hypotézy 11 v SPSS realizujeme cez zadanie:
- ANALYZE/ REGRESSION/ LINEAR, otvorilo sa dialógové okno, v ktorom môžeme zadať premenné. Závislú premennú (životnú spokojnosť) presunieme do voľného okna v časti DEPENDENT, prediktor (optimizmus) presunieme do okna INDEPENDENT(S). Na pravej strane označíme STATISTICS a po otvorení ponuky vyberieme Confidence intervals. Výsledkom výpočtu je niekoľko tabuliek.
Interpretáciu výsledku začíname tým, že zhodnotíme, či je regresná priamka adekvátnym modelom pre príslušné dáta, z toho dôvodu sa najskôr pozrieme na tabuľku Model Summary a tabuľku ANOVA. Vhodnými ukazovateľmi vhodnosti modelu sú hodnoty R a R2 (R Square). Hodnota R predstavuje viacnásobný korelačný koeficient37, v prípade dvoch premenných predstavuje párový korelačný koeficient (na tomto mieste nadobúda iba pozitívne hodnoty – nevyjadruje teda korelačný vzťah). Čim vyššiu hodnotu R dosahuje, tým si môžeme byť istejší, že model vyhovuje našim dátam. V tomto prípade sme dosiahli hodnotu R = 0,483.
R2 informuje o tom, aká presná je predikcia hodnôt závislej premennej podľa regresnej rovnice, ktorú sme pre danú hypotézu využili. Čim ďalej sú dáta rozložené od regresnej priamky, tým je chyba predikcie väčšia a R2 menšie (a naopak). R2 informuje o tom, aký tesný je lineárny regresný vzťah medzi dvoma premennými. V tomto prípade sme získali hodnotu R 2 = 0,233. Túto hodnotu môžeme vynásobiť 100 (rovnako ako v prípade korelačných koeficientov). Týmto postupom získame koeficient determinácie, znamená to, že 23,3% rozptylu životnej spokojnosti je vysvetliteľný/podmienený správaním premennej optimizmus
Výsledok v tabuľke ANOVA overuje vhodnosť modelu pre získané dáta, resp. overuje či využitý model predpovedá závislú premennú lepšie, ako keby sme namiesto nameraných hodnôt prediktoru využili údaj o priemere. Získali sme výsledok: F = 131,832; p = 0,001. Nakoľko je výsledok signifikantný (p < 0,05), usudzujeme, že vypočítaný regresný model je vhodný pre predikciu závislej premennej.
Samotná odpoveď na hypotézu 11 sa nachádza v tabuľke s názvom Coefficients. Daná tabuľka zobrazuje B koeficienty, ktoré sú zobrazené taktiež v bodovom grafe (Graf 16: y = 6,1 + 0,74x). Koeficienty zrealizovanej regresnej analýzy zobrazujú tú rovnicu regresnej analýzy, ktorá najlepšie predikuje životnú spokojnosť (y). Neštandardizované regresné koeficienty (B) sú vyjadrené v jednotkách, v ktorých boli namerané (v tomto prípade predstavujú skóre vo využitých dotazníkoch). Na druhej strane, štandardizovaný regresný koeficient je štandardizovaný tým spôsobom aby nadobúdal hodnoty od -1 po 1.
Pre interpretačné účely skontrolujeme signifikanciu, ktorá má dosahovať hodnotu p < 0.05. Pre regresný koeficient a regresnú konštantu môžeme konštatovať, že obidve p dosahujú hodnotu menšiu ako 0,05, znamená to, že sú štatisticky signifikantne odlišné od nuly.
Intervaly istoty predstavujú pravdepodobný rozptyl regresnej konštanty a regresného koeficientu v populácii, čím je náš odhad presnejší, tým sa horný a dolný interval istoty nachádza k sebe bližšie, dolný interval istoty regresného koeficientu optimizmu je 0,611 a horný interval je 0,863 (hodnoty sú si vcelku blízke a neblížia sa nule), z toho dôvodu môžeme náš záver považovať za spoľahlivý a významný i v populácii.
Interpretácia výsledkov H11:
Hypotéza 11 bola testovaná použitím jednoduchej lineárnej regresnej analýzy, ktorej výsledok uvádzame v Tabuľke 19. Testovali sme, či
optimizmus významne predikuje životnú spokojnosť. Získaný regresný model je: Životná spokojnosť = 6,096 + 0,737xOptimizmus. Regresná analýza bola štatisticky významná (R 2 = 0,233, F(1;433) = 131,832; p = 0,001). Zistili sme, že optimizmus významne predikuje životnú spokojnosť (Beta = 0,483; p = 0,001), z toho dôvodu hypotézu prijímame.
Tabuľka 19 Výsledky testovania H11: Jednoduchá lineárna regresná analýza (predikcia životnej spokojnosti)
| B | 95% CI | β | t | p | |
| Konštanta | 6,096 | [3,249; 8,942] | 4,209 | ,001 | |
| Optimizmus | 0,737 | [0,611; 0,863] | ,483 | 11,482 | ,001 |
Pozn.: R 2 adj = 0,232; CI = intervaly istoty pre B
12.2 Viacnásobná lineárna regresná analýza
Jednoduchá lineárna regresná analýza podlieha podobnému problému ako párová korelačná analýza, ktorým je prílišné zjednodušenie skutočnosti. Psychologická realita človeka je tvorená previazanosťou mnohých okolností, nie iba dvoch oblastí. Túto skutočnosť reflektuje viacnásobná lineárna regresná analýza, ktorá analyzuje vzťahy medzi viacerými prediktormi a jednou závislou premennou.
Výhodou viacnásobnej regresnej analýzy oproti jednoduchej lineárnej regresnej analýze je taktiež v odhade sily vzťahu medzi jednotlivým prediktorom a závislou premennou pri súčasnej kontrole pôsobenia ostatných prediktorov. Vďaka odhadu relatívnej sily vzťahu medzi jednotlivými prediktormi a závislou premennoudokážeme určiť, ktoré premenné majú na závislú premennú najväčší efekt, resp. ktoré premenné vysvetľujú najväčší rozptyl závislej premennej.
Viacnásobná lineárna regresná analýza podlieha niekoľkým podmienkam využitia, prvé tri sú totožné s podmienkami pre jednoduchú regresnú analýzu (linearita vzťahu medzi prediktormi a závislou premennou, závislá premenná meraná na intervalovej úrovni a normálne rozloženie pri menších výskumných vzorkách), avšak viacnásobná regresia zahŕňa navyše:
- Prediktory spolu nesmú korelovať príliš silne, pokiaľ by sa tak stalo výsledky regresnej analýzy by boli nespoľahlivé, multikolinearita (silná korelácia medzi prediktormi) spôsobuje, že vhodný prediktor sa pravdepodobne preukáže ako nevýznamný.
- Odľahlé hodnoty môžu narušiť odhad parametrov regresnej rovnice, z toho dôvodu sa v dátach nemôžu nachádzať.
- Chyby merania musia byť nezávislé (tento predpoklad je možné overiť Durbin – Watsonovým testom) a normálne rozložené (predpoklad je možné otestovať graficky ako súčasť lineárnej regresnej analýzy).
- Vzťahy medzi premennými vykazujú homoskedasticitu, čo znamená homogenitu rozptylov. Rozptyl v dátach jednej premennej dosahuje podobné hodnoty v druhej premennej (tento predpoklad taktiež testujeme graficky ako súčasť lineárnej regresnej analýzy).
Príklad 12 – kardinálne premenné:
H12: Predpokladáme, že optimizmus, seba úcta a miera vnímaného stresu
predikujú životnú spokojnosť .
Pred realizáciou výpočtu viacnásobnej regresnej analýzy overíme jej podmienky. Nakoľko všetky premenné sú merané na intervalovej úrovni (jedná sa o hrubé skóre štyroch dotazníkov) a výskumná vzorka je tvorená veľkým počtom participantov (N = 434), nie je potrebné overovať prítomnosť normálneho rozloženia.
Prvou podmienkou, ktorú potrebujeme skontrolovať, je linearita vzťahov medzi
prediktormi a závislou premennou. K tomuto účelu vytvoríme bodový maticový graf.
- GRAPHS/ CHART BUILDER, po ktorom bude otvorené dialógové okno pre výber grafu. V časti GALLERY je možné zvoliť vhodný typ grafu, v tomto prípade SCATTERPLOT MATRIX. Vľavo hore nájdeme hľadané premenné: optimizmus, sebaúcta, miera vnímaného stresu a životná spokojnosť. Všetky hľadané premenné označíme tlačidlom CTRL, čím sa umožní spoločný presun na os X. Stlačíme OK.
- Na zobrazený graf klikneme dvakrát, čím sa stane aktívnym a je možné robiť úpravy. Vyberieme možnosť FIT LINE AT TOTAL (druhý riadok v ponuke možností), vďaka čomu sa vytvoria regresné priamky pre všetky páry premenných. Výsledkom zadania je Graf 17, na základe ktorého môžeme pozorovať tvar vzťahu medzi prediktormi a životnou spokojnosťou. Nakoľko dané vzťahy približne kopírujú regresné priamky, je možné podmienku linearity považovať za splnenú a môžeme použiť viacnásobnú lineárnu regresnú analýzu
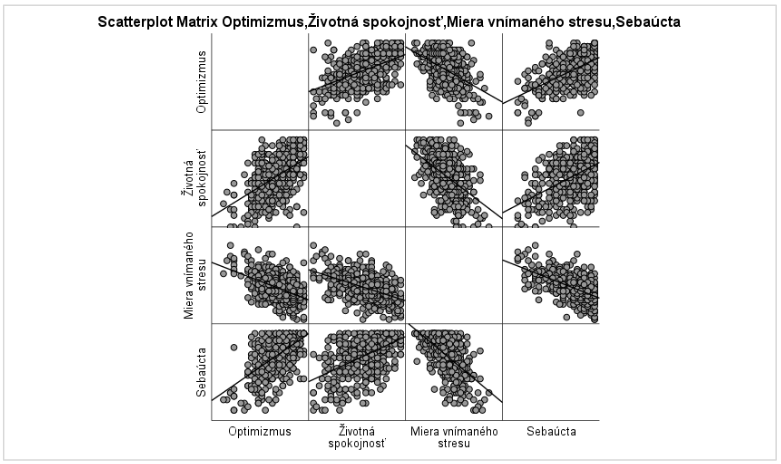
Graf 17 Bodový maticový graf zobrazujúci lineárny vzťah medzi prediktormi (optimizmus, miera prežívaného stresu, sebahodnota) a závislou premennou životná spokojnosť
Testovanie hypotézy 12 v SPSS realizujeme cez zadanie:
- ANALYZE/ REGRESSION/ LINEAR, otvorilo sa dialógové okno, v ktorom môžeme zadať premenné. Závislú premennú (životnú spokojnosť) presunieme do voľného okna v časti DEPENDENT, prediktory (optimizmus, miera vnímaného stresu, sebaúcta) presunieme do okna INDEPENDENT(S).
- Na pravej strane označíme STATISTICS a po otvorení ponuky vyberieme: Confidence intervals, Durbin-Watson, Casewise diagnostics, Descriptives, Collinearity diagnostics.
- Otvoríme ponuku PLOTS s cieľom vytvoriť grafické zobrazenie rozloženia chýb merania (nakoľko jednou z podmienok lineárnej regresnej analýzy je normálne rozloženie chýb merania): na os X umiestnime štandardizované predikované hodnoty (ZPRED) a na os Y umiestnime štandardizované rezíduá (ZRESID). Označíme Histogram alebo Normal probability plot. Výsledkom výpočtu je niekoľko tabuliek a grafov.
Prvé dve tabuľky, ktoré uvidíte pri tomto zadaní sú: (1) Descriptive Statistics, resp. deskriptívna tabuľka, v ktorej sú uvedené priemerné hodnoty všetkých premenných, ich štandardné odchýlky a veľkosť výskumnej vzorky. (2) Correlations, čiže korelačná matica pre všetky analyzované premenné. Tabuľku skontrolujeme, medzi nezávislými premennými by nemala nastať silná korelácia, konkrétne silnejšia ako 0,8 (v kladnom alebo zápornom smere) – jedná sa o prvotnú kontrolu multikolinearity, ktorá predstavuje jednu z podmienok pre realizáciu regresnej analýzy. V analyzovanom prípade je najsilnejšia korelácia 0,575 (medzi premennými sebahodnota a optimizmus), na základe čoho môžeme usúdiť, že medzi prediktormi nenastala kolinearita.
Rovnako ako v prípade jednoduchej lineárnej regresnej analýzy hodnotíme, či je aktuálne testovaný model adekvátnym modelom pre príslušné dáta, z toho dôvodu kontrolujeme tabuľku Model Summary a tabuľku ANOVA. Ukazovateľmi vhodnosti modelu sú hodnoty R a R 2 (R Square). Hodnota R predstavuje viacnásobný korelačný koeficient, tomto prípade sme dosiahli hodnotu R = 0,590.
R2 informuje o tom, aká presná je predikcia hodnôt závislej premennej podľa regresnej rovnice, ktorú sme pre danú hypotézu využili. V tomto prípade sme získali hodnotu R 2 = 0,348. Po jej vynásobení 100 získame koeficient determinácie: 34,8% rozptylu životnej spokojnosti je vysvetliteľný/podmienený správaním prediktorov. Durbin Watson koeficient zisťuje, či je predpoklad nezávislosti chýb merania obhájiteľný. Môže dosahovať hodnoty od 0 po 4. Interpretácia Durbin Watson koeficientu:
- DW < 1 – medzi chybami merania sa nachádza pozitívna korelácia,
- DW = < 1; 3 > – chyby merania sú relatívne nezávislé,
- DW = 2 – chyby merania spolu nekorelujú,
- DW > 3 – medzi chybami merania sa nachádza negatívna korelácia.
Durbin Watson koeficient v tomto prípade dosiahol hodnotu 1,864, znamená to, že sa daná hodnota nachádza v intervale od 1 po 3 (hodnota je blízka 2, ktorá predstavuje ideálny stav), čiže predpoklad nezávislosti chýb je obhájený.
Výsledok v tabuľke ANOVA overuje vhodnosť modelu pre získané dáta, resp. overuje či využitý model predpovedá závislú premennú lepšie, ako keby sme namiesto nameraných hodnôt prediktoru využili údaj o priemere. Výsledok analýzy: F = 75,955; p = 0,001. Každý signifikantný výsledok (p < 0,05) napovedá, že regresný model je vhodný pre predikciu závislej premennej životná spokojnosť.
Odpoveď na hypotézu 12 sa nachádza v tabuľke s názvom Coefficients (zobrazené sú regresná konštanta, regresné koeficienty a k nim prislúchajúce údaje). Koeficienty zrealizovanej regresnej analýzy zobrazujú tú rovnicu regresnej analýzy, ktorá najlepšie predikuje životnú spokojnosť (y). Neštandardizované regresné koeficienty (B) sú vyjadrené v jednotkách, v ktorých boli namerané (v tomto prípade predstavujú skóre vo využitých dotazníkoch). Ich prostredníctvom môžeme regresnú rovnicu vyjadriť takto: Životná spokojnosť = 13,541 + 0,383xOptimizmus – 0,302xMiera vnímaného stresu + 0,251xSebaúcta.
Na druhej strane, štandardizované regresné koeficienty sú vyjadrené tým spôsobom, aby dosahovali hodnoty od -1 po 1, čím sa umožní zhodnotiť relatívny význam každého prediktoru pre závislú premennú. Z tohto pohľadu má najväčší význam pre mieru životnej spokojnosti miera vnímaného stresu ( β = -0,261), ďalej optimizmus (β = 0,251) a napokon sebaúcta (β = 0,198). Ako je možné sledovať, rovnako ako v prípade korelačnej analýzy i regresné koeficienty môžu dosahovať kladné i záporné hodnoty. Miera vnímaného stresu má nepriamo úmerný vzťah so životnou spokojnosťou (nakoľko regresný koeficient nadobúda zápornú hodnotu) a ostatné prediktory majú kladný vzťah so životnou spokojnosťou. Pre interpretačné účely rovnako skontrolujeme signifikanciu, ktorá má dosahovať hodnotu p < 0.05. Pre regresnú konštantu a regresné koeficienty môžeme konštatovať, že všetky dosahujú hodnotu menšiu ako 0,05.
S možnosťou zovšeobecnenia našich zistení môžeme zohľadniť taktiež intervaly istoty, ktoré predstavujú pravdepodobný rozptyl regresnej konštanty a regresného koeficientu v populácii. Na tomto mieste sa môžeme pozrieť napr. na intervaly istoty regresného koeficientu miery vnímaného stresu, kde dolný interval dosahuje hodnotu je -0,413 a horný interval je -0,191, hodnoty nadobúdajú podobný charakter, celý pravdepodobnostný rozptyl koeficientu je záporný, znamená to, že v populácii sa pravdepodobne sledovaný regresný koeficient nebude rovnať nule, čím náš záver môžeme považovať za spoľahlivý. Rovnakým spôsobom skontrolujeme všetky intervaly istoty.
Po zadaní príkazu Collinearity diagnostics počas výpočtu regresnej analýzy sa súčasťou tabuľky Coefficients stala Štatistika kolinearity (uvedená na pravej strane). Skratka VIF znamená Variance Inflation Factor = faktor inflácie variancie a predstavuje diagnostické údaje o kolinearite. Minimálna hodnota VIF je 1 a predstavuje situáciu, kedy prediktory spolu vôbec nekorelujú. Čím vyššiu hodnotu nadobudne, tým existuje silnejšia korelácia medzi prediktormi, resp. tým je väčšia šanca multikolinearity. Ako zhodnotíme VIF? Základné princípy:
- VIF má hodnotu 1 – prediktory spolu nekorelujú,
- VIF má hodnotu medzi 1 a 5 – prediktory spolu korelujú stredne silne,
- VIF má hodnotu väčšiu ako 5 – prediktory spolu korelujú silne.
Znamená to, že každá hodnota väčšia ako 5 predstavuje situáciu, ktorú je potrebné dôkladne skontrolovať, avšak hodnota VIF väčšia ako 10 pre ktorýkoľvek prediktor znamená istotu prítomnej multikolinearity. Využiť multikolineárny prediktor má za dôsledok nespoľahlivú regresnú analýzu, prípadne sa dobrý prediktor preukáže ako nevýznamný. Najväčšiu hodnotu VIF dosahuje premenná sebahodnota (VIF = 1,816), môžeme konštatovať neprítomnosť multikolinearity.
V závere analýzy skontrolujeme zobrazené graficky testované vlastnosti: Normálne rozloženie chýb merania testujeme prostredníctvom histogramu reziduí (Graf 18). Môžeme konštatovať, že histogram reziduí sa blíži normálnemu rozloženiu (s väčším rezíduom na pravej strane, v tomto prípade sa jednalo o prípad so zistenou hodnotou štandardného rezídua -3,354, toto narušenie podmienky je potrebné skontrolovať 38.
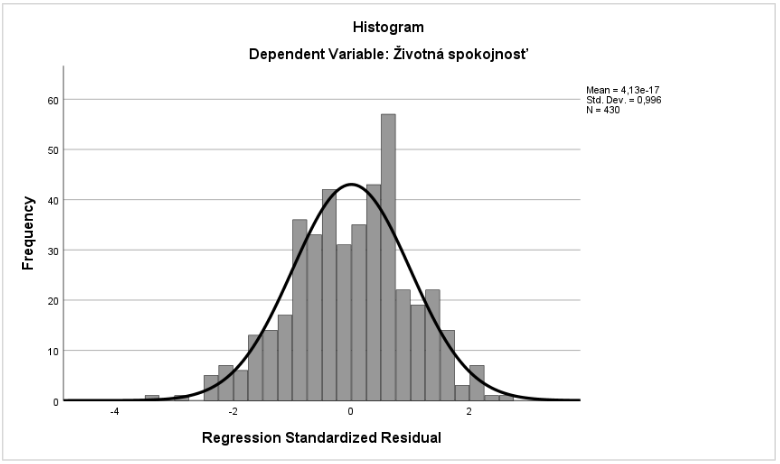
Graf 18 Histogram reziduí testujúci normálne rozloženie reziduí
Následne skontrolujeme predpoklad homoskedasticity prostredníctvom bodového grafu zobrazujúceho vzťah štandardizovaných rezíduí a štandardizovanej predikovanej hodnoty závislej premennej. Daný graf testuje či je roz ptyl chýb merania konštantný v regresnom modeli. Ak je rozptyl homoskedastický, model bol dobre definovaný (tip: ak by preukázal opak zvyčajne pomôže pridanie ďalšieho prediktoru).
Homoskedasticita sa vizuálne prejaví tak, že body grafu by nemali vykazovať žiadny vzorec usporiadania (napr. zhlukovanie sa do skupín, alebo tvar pripomínajúci L, U…). V analyzovanom prípade môžeme potvrdiť zachovanie podmienky homoskedasticity (Graf 19).
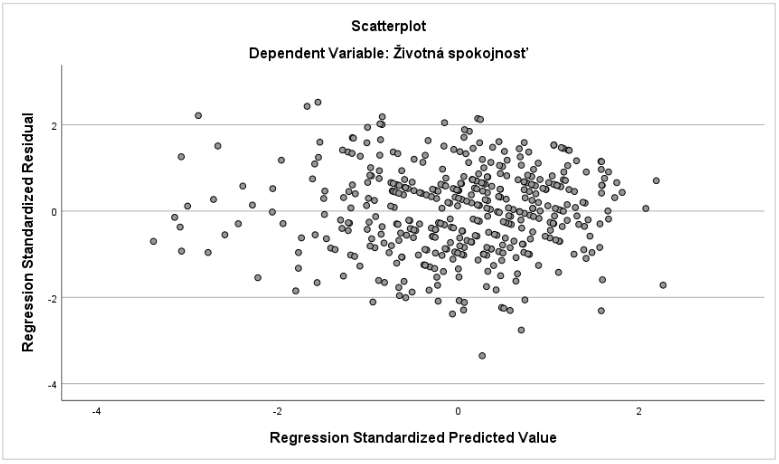
Graf 19 Bodový graf vzťahu štandardizovaných rezíduí a štandardizovanej predikovanej hodnoty závislej premennej
Hypotéza 12 bola testovaná použitím viacnásobnej lineárnej regresnej analýzy, ktorej výsledok uvádzame v Tabuľke 20. Testovali sme predikčný potenciál optimizmu, miery vnímaného stresu a sebaúcty voči životnej spokojnosti. Získaný regresný model môžeme vyjadriť prostredníctvom nasledovnej schémy:
Životná spokojnosť = 13,541 + 0,383xOptimizmus – 0,302xMiera vnímaného stresu + 0,251xSeba úcta.
Kontrola predpokladov: Pred preskúmaním predikčnej sily nášho modelu sme vykonali dôkladné posúdenie jeho základných predpokladov, aby sme potvrdili integritu našej analýzy. Prostredníctvom bodových grafov sme overili linearitu prediktorov so závislou premennou, pričom sme neodhalili žiadne odchýlky od lineárnych očakávaní. Okrem toho Durbin- Watson koeficient dosiahol hodnotu 1,864, čím sa účinne vylúčila autokorelácia medzi rezíduami a potvrdila sa nezávislosť chýb. Faktor inflácie variancie (VIF) bol pre každý prediktor hlboko pod prahom 5, najvyššia hodnota bola 1,816 pre premennú sebaúcta, čo rozptýlilo obavy z multikolinearity.Vizuálnou kontrolou histogramu rezíduí bolo potvrdené kritérium normality rezíduí a súčasne kontrolou bodového grafu štandardizovaných predikovaných hodnôt a rezíduí bola potvrdená homoskedasticita. Súhrnne tieto diagnostické testy potvrdili kľúčové predpoklady, na ktorých je založený náš viacnásobný lineárny regresný model, a poskytli tak solídny základ pre následnú analýzu.
Zhrnutie modelu: Celková zhoda modelu bola štatisticky významná, čo naznačuje F -štatistika 75,955 s hodnotou p menšou ako 0,001 (F(3,426) = 75,955, p < 0,001), znamená to, že model vysvetľuje významnú časť rozptylu závislej premennej životná spokojnosť. Následne, hodnota R² 0,348 ilustruje, že náš model predstavuje približne 35% variability životnej spokojnosti, čo potvrdzuje význam zahrnutých prediktorov. Zistili sme, že optimizmus ( β = 0,251; p =0,001), miera vnímaného stresu ( β = -0,261; p = 0,001) a seb ahodnota ( β = 0,198; p = 0,001) významne predikujú životnú spokojnosť, z toho dôvodu hypotézu prijímame.
Tabuľka 20 Výsledky testovania H12: Viacnásobná lineárna regresná analýza (predikcia životnej spokojnosti)
| B | 95% CI | Beta | t | p | |
| Konštanta | 13,541 | [7,056; 20,025] | 4,104 | ,001 | |
| Optimizmus | 0,383 | [0,236; 0,529] | ,251 | 5,137 | ,001 |
| Miera vnímaného stresu | -0,302 | [-0,413; -0,191] | -,261 | -5,344 | ,001 |
| Sebaúcta | 0,251 | [0,120; 0,382] | ,198 | 3,757 | ,001 |
Za určitých okolností nás vo viacnásobnej lineárnej regresnej analýze môže zaujímať i predikčný potenciál nominálnej premennej. Podmienkou pre realizáciu takéhoto riešenia je, aby nominálna premenná bola dichotomická (resp. dosahovala dve možné hodnoty). Nasledujúci príklad sa týka spomínaného riešenia:
Príklad 13 – kardinálne prediktory a nominálny prediktor:
H13: Predpokladáme, že miera vnímaného stresu, pozitívna afektivita a
pohlavie predikujú životnú spokojnosť.
Hypotézu je možné rozdeliť na niekoľko častí resp. podhypotéz, napr. týmto spôsobom:
H13a: Predpokladáme, že miera vnímaného stresu predikuje životnú spokojnosť negatívne (jednosmerná hypotéza).
H13b: Predpokladáme, že pozitívna afektivita a pohlavie predikujú životnú spokojnosť pozitívne (jednosmerná hypotéza).
Rovnako ako v predchádzajúcom príklade, potrebujeme pred realizáciou výpočtu overiť jej podmienky. Jedná sa o rovnakú výskumnú databázu, vieme teda, že vo veľkej výskumnej vzorke nie je potrebné testovať normálne rozloženie a zároveň, že všetky premenné s výnimkou pohlavia (nominálna premenná) sú merané na intervalovej úrovni. Overíme predpoklad linearity medzi prediktormi a závislou premennou. Nakoľko pohlavie predstavuje nominálnu premennú, daná podmienka sa naň nevzťahuje.
Vytvoríme bodový maticový graf cez zadanie (na tomto mieste si ukážeme iný spôsob zadania bodového grafu ako v predchádzajúcom prípade):
Testovanie linearity v SPSS realizujeme cez zadanie:- GRAPHS/ SCATTER/ DOT, po ktorom bude otvorené dialógové okno pre výber grafu, zvolíme MATRIX SCATTER. Vľavo nájdeme hľadané premenné: miera vnímaného stresu, pozitívna afektivita a životná spokojnosť (nominálnu premennú pohlavie zobrazovať potrebné nie je). Presunieme ich na voľné miesto s nadpisom Matrix Variables. Stlačíme OK.
- Na zobrazený graf klikneme dvakrát, graf sa otvorí v novom okne a je možné robiť úpravy. Vyberieme možnosť FIT LINE AT TOTAL s cieľom vytvoriť regresné priamky pre všetky páry premenných. Ako je možné vidieť na Grafe 20 dané vzťahy približne kopírujú regresné priamky, na základe čoho podmienku linearity považujeme za splnenú.
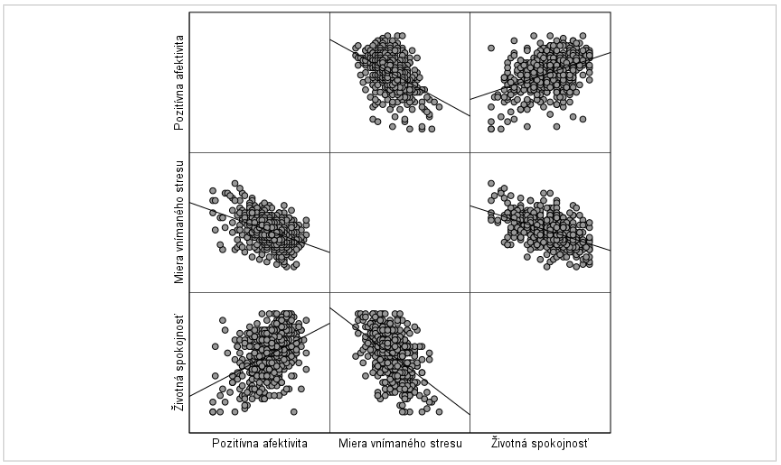
Graf 20 Bodový maticový graf zobrazujúci lineárny vzťah medzi prediktormi (miera vnímaného stresu, pozitívna afektivita) a závislou premennou životná spokojnosť
Testovanie hypotézy 13 v SPSS realizujeme cez zadanie:
- ANALYZE/ REGRESSION/ LINEAR, otvorilo sa dialógové okno, v ktorom môžeme zadať premenné. Závislú premennú (životnú spokojnosť) presunieme do voľného okna v časti DEPENDENT, prediktory (miera vnímaného stresu, pozitívna afektivita, pohlavie) presunieme do okna INDEPENDENT(S).
- Na pravej strane označíme STATISTICS a vyberieme: Confidence intervals, Durbin-Watson, Casewise diagnostics, Descriptives, Collinearity diagnostics (samozrejme, možností je viac, daný zoznam možností predstavuje základ pre kvalitné prevedenie regresnej analýzy). V ponuke PLOTS vytvoríme grafické zobrazenie rozloženia chýb merania (testujeme normálne rozloženie chýb merania): na os X umiestnime štandardizované predikované hodnoty (ZPRED) a na os Y umiestnime štandardizované rezíduá (ZRESID). Označíme Histogram alebo Normal probability plot (výber grafu závisí od Vašej preferencie, jedná sa o testovanie rovnakej podmienky). Výsledkom výpočtu je niekoľko tabuliek a grafov.
Pri kontrole deskriptívnej štatistiky riešenej úlohy vidíme priemerné hodnoty všetkých premenných, ich štandardné odchýlky a veľkosť výskumnej vzorky. Skontrolujeme korelačnú maticu, cieľom je zistiť či sa medzi prediktormi nachádza korelácia silnejšia ako ±0,8, v takom prípade by sa jednalo o multikolinearitu. V analyzovanom prípade je najsilnejšia korelácia -0,442 (medzi premennými miera vnímaného stresu a pozitívna afektivita), resp. medzi prediktormi nenastala kolinearita.
Kontrolou tabuľky označenej Model Summary zhodnotíme, či je testovaný model adekvátnym modelom pre dáta, konkrétne prostredníctvom hodnôt R a R 2 (R Square). Viacnásobný korelačný koeficient dosahuje hodnotu R=0,561 s jeho umocnenou hodnotou je R 2 = 0,314. Vynásobením R 2 x 100 získame koeficient determinácie: 31,4% rozptylu životnej spokojnosti je podmienený správaním prediktorov. Súčasťou zobrazených výsledkov je adjustovaná hodnota R 2 (resp. prispôsobené R2), ktorá vyjadruje rozptyl závislej premennej, ktorý je vysvetliteľný prediktormi v populácii (má teda zovšeobecňujúci charakter). V danej analýze dosahuje Durbin Watson koeficient hodnotu 1,877, zisťuje, či je predpoklad nezávislosti chýb merania obhájiteľný a s ohľadom na jeho hodnotu bola podmienka naplnená.
Výsledok analýzy variancie (tabuľka ANOVA), ktorý overuje vhodnosť modelu pre získané dáta má hodnoty: F = 65,577; p = 0,001. Nakoľko sme dosiahli signifikantný výsledok (p < 0,05), regresný model je vhodný pre predikciu závislej premennej životná spokojnosť.
Odpoveď na hypotézu 13 sa nachádza v tabuľke Coefficients. Koeficienty zrealizovanej regresnej analýzy zobrazujú tú rovnicu regresnej analýzy, ktorá najlepšie predikuje životnú spokojnosť (y), resp. dosahuje najmenšiu chybu odhadu. Prostredníctvom neštandardizovaných regresných koeficientov (B) môžeme finálnu regresnú rovnicu vyjadriť takto: Životná spokojnosť = 24,527 – 0,477xMiera vnímaného stresu + 0,220xPozitívna afektivita + 1,994xPohlavie.Nakoľko štandardizované regresné koeficienty umožňujú zhodnotiť relatívny význam každého prediktoru pre závislú premennú, môžeme konštatovať, že najväčší význam pre mieru životnej spokojnosti predstavuje v negatívnom smere miera vnímaného stresu (β = -0,411), nasleduje (v kladnom smere) pozitívna afektivita (β = 0,235) a napokon pohlavie (β = 0,145). Ako interpretovať prediktívny význam nominálnej premennej? V prvom rade si musíme uvedomiť, že regresná analýza je založená na korelačnej analýze a korelačný koeficient medzi dichotomickou nominálnom premennou a kardinálnou premennou je bežnou súčasťou psychologických výskumov (konkrétne by sa v prípade korelačnej analýzy jednalo o bodovo biseriálny korelačný koeficient). K danému regresnému vzťahu môžeme pristupovať analogicky. Premenná pohlavie dosahuje dve možné hodnoty/kategórie: 1 = Muž, 2 = Žena. Medzi pohlavím a životnou spokojnosťou sme zistili kladný predikčný vzťah, čo znamená, že kategória premennej, ktorá má vyššiu hodnotu (v tomto prípade 2 = Žena) je pozitívne asociovaná so závislou premennou, resp. ženy zažívajú vyššiu mieru životnej spokojnosti. Pre interpretačné účely skontrolujeme tiež signifikanciu, ktorá dosahuje hodnotu p < 0.05 pre všetky vybrané prediktory a aj regresnú konštantu.
Následne sa zameriame na intervaly istoty, ktoré predstavujú pravdepodobný rozptyl regresnej konštanty a regresného koeficientu v populácii. V tomto príklade skontrolujeme intervaly istoty regresného koeficientu pozitívnej afektivity, kde dolný interval dosahuje hodnotu je 0,138 a horný interval hodnotu 0,303, hodnoty sú pozitívne, nenadobúdajú hodnotu 0, znamená to, že v populácii sa daný regresný koeficient s pravdepodobnosťou 95% nebude rovnať nule, z toho dôvodu záver môžeme považovať za spoľahlivý. Následne skontrolujeme všetky intervaly istoty. Súčasťou tabuľky Coefficients je Štatistika kolinearity (Collinearity Statistics). Faktor inflácie variancie (VIF) ako diagnostické kritérium o prítomnosti kolinearity je nevyhnutnou súčasťou overovania vlastností viacnásobnej regresnej analýzy s ohľadom na potenciálne dôsledky využívania kolineárnych prediktorov (nespoľahlivé výsledky regresnej analýzy, nevýznamné hodnoty regresných koeficientov i napriek schopnosti prediktorov predikovať závislú premennú). Najväčšiu hodnotu VIF dosahuje premenná miera vnímaného stresu (VIF = 1,274), avšak jedná sa o zanedbateľnú hodnotu (nakoľko je hlboko pod hodnotou 5).
Podmienky, ktorých plnenie je ďalej potrebné skontrolovať, sú normálne rozloženie chýb merania a homoskedasticita. Viacnásobná regresná analýza poskytuje vizuálnu kontrolu daných podmienok ako súčasť analýzy (možností je určite viac, podmienky je možné kontrolovať taktiež prostredníctvom testov štatistickej významnosti, v prípade záujmu je možné pozrieť vhodné publikácie). Normálne rozloženie chýb merania testujeme prostredníctvom histogramu reziduí. Konštatujeme, že histogram reziduí (Graf 21) zobrazuje normálne rozloženie chýb merania.
Predpoklad homoskedasticity sme overili prostredníctvom bodového grafu zobrazujúceho vzťah štandardizovaných rezíduí a štandardizovanej predikovanej hodnoty závislej premennej. Daný graf testuje či je rozptyl chýb merania konštantný v regresnom modeli. V analyzovanom prípade môžeme potvrdiť zachovanie podmienky homoskedasticity (Graf 22).
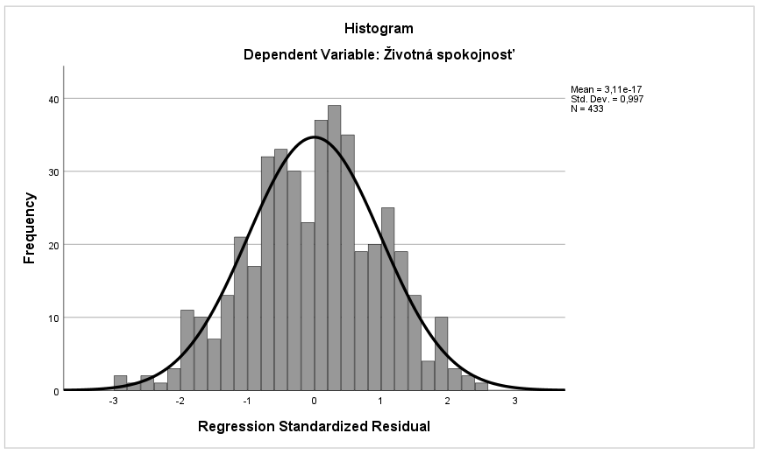
Graf 21 Histogram reziduí testujúci normálne rozloženie reziduí
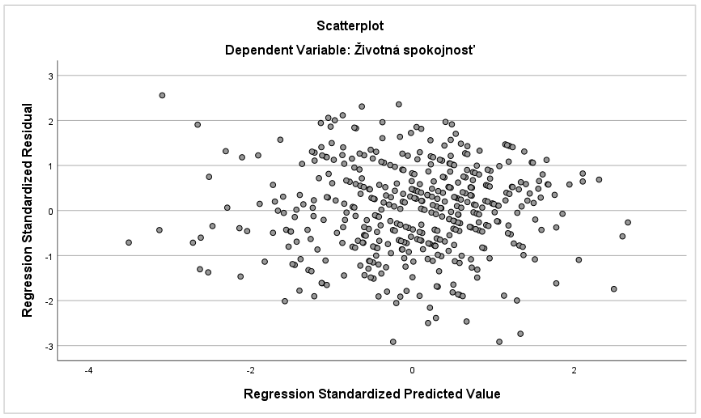
Graf 22 Bodový graf vzťahu štandardizovaných rezíduí a štandardizovanej predikovanej hodnoty závislej premennej
Hypotéza 13 bola testovaná použitím viacnásobnej lineárnej regresnej analýzy, ktorej výsledok uvádzame v Tabuľke 21. Testovali sme predikčný potenciál miery vnímaného stresu, pozitívnej afektivity a pohlavia voči životnej spokojnosti. Získaný regresný model môžeme vyjadriť prostredníctvom nasledovnej schémy:
Životná spokojnosť = 24,527 – 0,477xMiera vnímaného stresu + 0,220xPozitívna afektivita + 1,994xPohlavie.
Kontrola predpokladov: Pred preskúmaním predikčnej sily regresného modelu sme vykonali posúdenie jeho základných predpokladov, aby sme potvrdili integritu našej analýzy. Prostredníctvom bodových grafov sme overili linearitu prediktorov so závislou premennou a nezistili sme narušenie danej podmienky. Durbin- Watson koeficient dosiahol hodnotu 1,877, na základe tohto faktu vyvodzujeme, že autokorelácia medzi rezíduami nie je prítomná a potvrdila sa nezávislosť chýb. Faktor inflácie variancie (VIF) na nachádzal pod prahom 5, najvyšš ia hodnota bola 1,274 pre premennú miera vnímaného stresu, na základe čoho je možné vyhodnotiť, že každý prediktor pridáva svoju unikátnu varianciu pri predikcii závislej premennej. Vizuálnou kontrolou histogramu rezíduí bolo potvrdené kritérium normality rezíduí a súčasne kontrolou bodového grafu štandardizovaných predikovaných hodnôt a rezíduí bola potvrdená homoskedasticita 39. Súhrnne tieto diagnostické testy potvrdili predpoklady, na ktorých je založený aktuálne testovaný viacnásobný lineárny regresný model, a poskytli tak solídny základ pre následnú analýzu.
Zhrnutie modelu: elková zhoda modelu bola štatisticky významná, čo naznačuje F -štatistika 65,577 s hodnotou p menšou ako 0,001 (F(3,429) = 65,577, p < 0,001), znamená to, že model vysvetľuje významnú časť rozptylu závislej premennej životná spokojnosť. Hodnota R² rovnajúca sa 0,314 ilustruje, že náš model predstavuje približne 31% variability životnej spokojnosti, čo potvrdzuje význam zahrnutých prediktorov. Zistili sme, že miera vnímaného stresu ( β = - 0,411; p = 0,001), pozitívna afektivita ( β = 0,235; p = 0,001) a pohlavie ( β = 0,1145; p = 0,001) významne predikujú životnú spokojnosť, z toho dôvodu hypotézu prijímame. Navyše, prostredníctvom intervalov istoty predpokladáme, že daný výsledok by sa potvrdil taktiež v základnej populácii.
Tabuľka 21 Výsledky testovania H13: Viacnásobná lineárna regresná analýza (predikcia životnej spokojnosti)
| B | 95% CI | Beta | t | p | |
| Konštanta | 24,527 | [19,724; 29,330] | 10,036 | ,001 | |
| Miera vnímaného stresu | -0,477 | [-0,579; -0,374] | -,411 | -9,100 | ,001 |
| Pozitívna afektivita | 0,220 | [0,138; 0,303] | ,235 | 5,265 | ,001 |
| Pohlavie | 1,994 | [0,903; 3,085] | ,145 | 3,593 | ,001 |
12.3 Rôzne formy viacnásobnej lineárnej regresnej analýzy
Existujú rôzne možnosti akým spôsobom uskutočniť viacnásobnú regresnú analýzu. Rozhodnutie, ktorú metódu využiť, leží v možnosti predikcie štruktúry vzťahov. Na tomto základe sú postavené dva modely viacnásobnej regresnej analýzy:
- Deskriptívny model viacnásobnej regresnej analýzy – nepredpokladáme štruktúru vzťahov medzi prediktormi. Cieľom tohto typu regresnej analýzy je popis efektu, ktorý prediktory na závislú premennú majú. Overuje, aký
veľký podiel rozptylu závislej premennej je vysvetliteľný pomocou prediktorov. Pre predstavu uvádzame taktiež vizualizáciu deskriptívneho modelu (Obrázok 2).

Obrázok 2 Deskriptívny model viacnásobnej regresnej analýzy
- Kauzálny model viacnásobnej regresnej analýzy (tento typ analýzy sa nazýva kauzálny, avšak skontrolujte text vyššie pre priblíženie otázky, či regresná analýza dokáže zistiť kauzalitu vzťahov) – v tomto prípade predpokladáme konkrétnu
štruktúru vzťahov (medzi prediktormi vzájomne a taktiež voči závislej premennej).
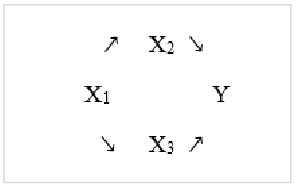
Obrázok 3 Kauzálny model viacnásobnej regresnej analýzy
Existujú dve hlavné alternatívy, akým spôsobom zostaviť model regresnej analýzy (deskriptívny a kauzálny) a súčasne existuje niekoľko možností ako premenné do výpočtu vložiť:
- Štandardná metóda (Enter method) – všetky premenné sú do výpočtu vložené súčasne. Jedná sa teda o metódu, ktorá je v súlade s deskriptívnym modelom regresnej analýzy. Tento typ analýzy umožňuje zistiť aký veľký podiel rozptylu závislej premennej je vysvetlený prediktormi (R 2), aký veľký efekt má každý prediktor na závislú premennú pri kontrole efektu ostatných prediktorov (neštandardizované regresné koeficienty) a napokon aká je relatívna dôležitosť každého prediktoru (štandardizované regresné koeficienty).
- Metóda postupného vkladania (Stepwise method) – prediktory sú do výpočtu regresnej analýzy vkladané na základe matematických kritérií. Výskumník premenné môže vložiť súčasne avšak výpočet zobrazí niekoľko modelov, pričom do prvého modelu je zahrnutá regresná konštanta a prediktor, ktorý predikuje závislú premennú najlepšie. Znamená to, že o poradí premenných nerozhodne výskumník ale predikčný potenciál jednotlivých prediktorov. Prediktory, ktoré korelujú so závislou premennou nevýznamne sa v regresnom modely nezobrazia. Metódu postupného vkladania využívame pokiaľ je naším cieľom maximalizovať predikciu s čo možno najmenším počtom prediktorov.
- Hierarchická metóda (Blocks method) – poradie vstupu premenných do regresnej analýzy riadi výskumník, premenné v tomto prípade pridávame v skupinách (blokoch) na základe nášho predpokladu o vzťahoch medzi prediktormi vzájomne a o vzťahoch medzi prediktormi a závislou premennou. Výskumník rozhoduje o tom, či využije v jednotlivých skupinách (blokoch) štandardnú metódu alebo metódu postupného vkladania. Jedná sa o metódu, ktorá je v súlade s kauzálnym modelom regresnej analýzy.
Nasledujúci príklad viacnásobnej regresnej analýzy budeme realizovať prostredníctvom metódy postupného vkladania aby ste mali príležitosť vidieť v akých aspektoch sa tento typ regresnej analýzy líši od štandardnej metódy, ktorou boli riešené hypotézy 12 a 13. Nakoľko princíp metódy postupného vkladania je založený na štatistických kritériách, a nie na predchádzajúcich výskumoch či teórii, jedná sa o exploračnú metódu, čo znamená, že pri jej realizácii netestujeme hypotézu ale kladieme výskumnú otázku. Z toho dôvodu, pokiaľ existujú výskumy, ktoré predchádzajú váš výskumný zámer v podobných podmienkach, je lepšou voľbou štandardná metóda alebo hierarchická metóda (v závislosti od toho či predpokladáme štruktúru vzájomných vzťahov medzi prediktormi a taktiež voči závislej premennej).
Príklad 14 – kardinálne prediktory a nominálny prediktor realizované prostredníctvom metódy postupného vkladania:
O: Predikuje optimizmus, sebaúcta, sociálna žiadúcnosť a pohlavie zvládanie života?
Pred realizáciou výpočtu overíme podmienky viacnásobnej regresnej analýzy: jedná sa o veľkú výskumnú vzorku a zároveň všetky premenné s výnimkou pohlavia sú merané na intervalovej úrovni. Overíme predpoklad linearity medzi prediktormi a závislou premennou prostredníctvom maticového grafu (Graf 23). Ako je možné vidieť, skúmané vzťahy nemajú viditeľný nelineárny tvar.
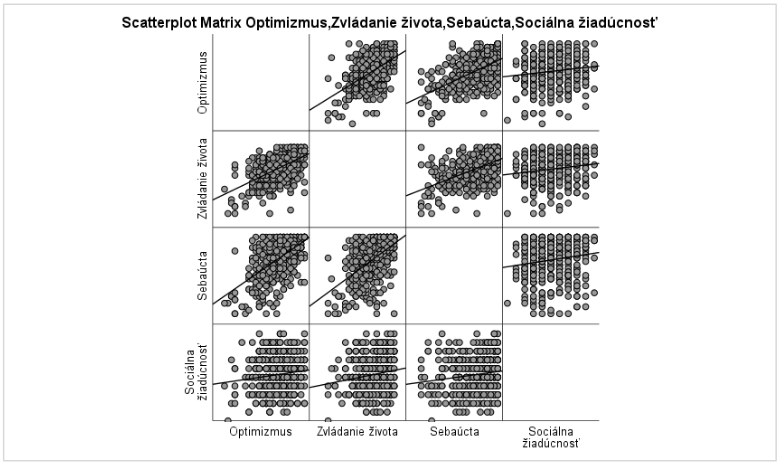
Graf 23 Bodový maticový graf zobrazujúci lineárny vzťah medzi prediktormi (optimizmus, sebaúcta, sociálna žiadúcnosť) a závislou premennou zvládania života
Testovanie výskumnej otázky v SPSS realizujeme cez zadanie:
- ANALYZE/ REGRESSION/ LINEAR, v dialógovom okne zadáme premenné. Závislú premennú (zvládanie života) presunieme do okna v časti DEPENDENT, prediktory (optimizmus, sebaúcta, sociálna žiadúcnosť, pohlavie) presunieme do okna pod ňou.
- Pod prediktormi je prednastavená štandardná metóda (Method: Enter), túto možnosť je možné upraviť, po otvorení ponuky vybrať možnosť STEPWISE (metódu postupného vkladania, v ponuke sa nachádzajú ešte ďalšie možnosti: Remove, Backward, Forward, jedná sa o podtypy metódy postupného vkladania).
- Na pravej strane označíme STATISTICS a vyberieme: Confidence intervals, Durbin-Watson, Casewise diagnostics, R squared change, Descriptives, Collinearity diagnostics (prípadne ďalšie).
- V ponuke PLOTS vytvoríme grafické zobrazenie rozloženia chýb merania: os X – štandardizované predikované hodnoty (ZPRED) a os Y – štandardizované rezíduá (ZRESID). Označíme Histogram alebo Normal probability plot.
Môžeme skontrolovať korelačnú maticu s cieľom zistiť či sa medzi prediktormi nachádza korelácia silnejšia ako ±0,8, v takom prípade by sa jednalo o multikolinearitu, nakoľko však najsilnejšia korelácia dosiahla hodnotu 0,569 (medzi premennými sebaúcta a optimizmus) usudzujeme, že medzi prediktormi nenastala kolinearita.
Nasledujúca tabuľka Variables Entered/Removed informuje o pridaných premenných do regresnej analýzy (pokiaľ by sa jednalo o štandardnú metódu, nachádzali by sa tu všetky prediktory bez ohľadu na predikčný potenciál voči závislej premennej), v aktuálnom príklade zisťujeme, že premenná sociálna žiadúcn osť sa v modely regresnej analýzy nenachádza, nakoľko nenaplnila štatistické kritérium pre zaradenie do modelu (nepredikuje významne závislú premennú).
Kontrolou tabuľky Model Summary (sumár modelu) hodnotíme adekvátnosť modelu pre dáta, vyobrazenie tohto výsledku má iný charakter ako v štandardnej metóde (viď. tabuľka 22). Metóda postupného vkladania je charakteristická tým, že pridáva prediktory do regresného modelu po jednom, vďaka čomu môžeme vyhodnotiť okrem R, R 2 a adj. R 2, taktiež zmenu R2 pre každý prediktor samostatne a vyhodnotenie významnosti takejto zmeny (Sig. F Change).
Nakoľko metóda postupného vkladania zoraďuje prediktory od takého, ktorý vysvetľuje najväčší rozptyl závislej premennej po taký, ktorý vysvetľuje najmenší rozptyl závislej premennej, môžeme skonštatovať, že najväčší rozptyl zvládania života vysvetľuje správanie premennej optimizmus (model 1). Na základe koeficientu determinácie (R2 x 100) je zrejmé, že 29,7% rozptylu zvládania života je podmienený správaním premennej optimizmus. Ďalej, optimizmus a sebaúcta spoločne (model 2) vysvetľujú 37,2% rozptylu závislej premennej. Individuálny efekt sebaúcty na zvládanie života je tým pádom 7,5% (R Square Change). Akým spôsobom sme na daný výsledok prišli?
R Square Change = R22 model – R21 model
0,075 = 0,372 – 0,297
R Square Change x 100 = Koeficient determinácie
0,075 x100 = 7,5 %
Obdobným spôsobom zisťujeme, že pohlavie je zodpovedné za 1,1% rozptylu pri predikcii zvládania života. Všetky prediktory spoločne vysvetľujú 38,3% rozptylu závislej premennej. V danej analýze dosahuje Durbin Watson koeficient hodnotu 1,951, usudzujeme teda na nezávislosť chýb merania.
Tabuľka 22 Sumár modelu výskumnej otázky: Viacnásobná lineárna regresná analýza (predikcia zvládania života)
| Model | R | R2 | Adj. R2 | R Square Change | Sig. F Change |
| 1 | ,545 | ,297 | ,296 | ,297 | ,001 |
| 2 | ,610 | ,372 | ,369 | ,075 | ,001 |
| 3 | ,619 | ,383 | ,378 | ,011 | ,007 |
- Regresná konštanta, Optimizmus
- Regresná konštanta, Optimizmus, Sebaúcta
- Regresná konštanta, Optimizmus, Sebaúcta, Pohlavie
Výsledky analýzy rozptylu (tabuľka ANOVA), ktoré overujú vhodnosť modelu pre získané dáta sú obdobne ako v sumáre modelu rozdelené na tri časti, pričom každá časť sa venuje jednému modelu (počet jednotlivých častí teda závisí na počte významných prediktorov). Pre účely interpretácie postačuje vyhodnotiť hodnoty finálneho modelu (v tomto prípade tretieho): F = 88,029; p = 0,001. Nakoľko sme dosiahli signifikantný výsledok (p < 0,05), regresný model je vhodný pre predikciu závislej premennej zvládanie života.
Odpoveď na analyzovanú výskumnú otázku sa nachádza v tabuľke Coefficients. Koeficienty zrealizovanej regresnej analýzy zobrazujú rovnice regresnej analýzy, ktoré významne predikujú zvládanie života (y). Sociálna žiadúcnosť sa z toho dôvodu v žiadnom výsledku nenachádza. Rovnice v jednotlivých modeloch sa môžu líšiť, nakoľko pridanie každého prediktoru ovplyvňuje rozptyl modelu (prediktory totiž spolu korelujú). Prostredníctvom neštandardizovaných regresných koeficientov (B) môžeme finálnu regresnú rovnicu vyjadriť takto: Zvládanie života = 8,226 + 0,324xOptimizmus + 0,230xSebaúcta – 0,828xPohlavie. Štandardizované regresné koeficienty umožňujú zhodnotiť relatívny význam každého prediktoru pre závislú premennú, môžeme konštatovať, že najväčší význam pre mieru pocitu zvládania života predstavuje v kladnom smere optimizmus ( β = 0,367) a sebaúcta (β = 0,318). Medzi pohlavím a zvládaním života je záporný predikčný vzťah (β = -0,104), nakoľko premenná pohlavie dosahuje dve možné kategórie (1 = Muž, 2 = Žena) znamená to, že kategória premennej, ktorá má vyššiu hodnotu (v tomto prípade 2 = Žena) je záporne asociovaná so závislou premennou, resp. ženy zažívajú nižšiu mieru pocitu zvládania života. V prípade danej analýzy je kontrola signifikancie uvedenej pri všetkých prediktoroch iba formálna, nakoľko metóda postupného vkladania zobrazuje iba tie prediktory, ktoré významne predikujú závislú premennú.
Súčasťou tabuľky Coefficients je Štatistika kolinearity (Collinearity Statistics). Faktor inflácie variancie (VIF) diagnostikuje prítomnosť kolinearity a najväčšiu hodnotu VIF dosahuje premenná sebaúcta (VIF = 1,496), jedná sa o zanedbateľnú hodnotu (nakoľko je hlboko pod hodnotou 5).
Tabuľka Excluded Variables poskytuje informáciu o vyradených premenných z analýzy a prislúchajúcich štatistikách (β, t, Sig, štatistika kolinearity).
Tabuľka Casewise Diagnostics (diagnostika prípadov) zobrazuje všetky prípady, ktoré vykazujú veľké štandardné rezíduum (odchýlku) predikovanej závislej premennej, konkrétne všetky prípady, ktoré dosahujú odchýlku väčšiu ako 3. Nakoľko viacnásobná regresná analýza môže byť ovplyvnená týmito prípadmi, je potrebné ich vplyv diagnostikovať (viď text vyššie ohľadom štatistiky DF Beta).
Podmienky, ktorých plnenie je ďalej potrebné skontrolovať, sú normálne rozloženie chýb merania a homoskedasticita. Normálne rozloženie chýb merania testujeme prostredníctvom histogramu reziduí. Ako už preukázala diagnostika prípadov, taktiež v histograme rezíduí závislej premennej môžeme pozorovať väčšiu štandardnú odchýlku ako 3 (jedná sa o dva prípady na ľavej strane rozloženia a jeden vplyvný prípad na pravej strane rozloženia), histogram však vykazuje relatívne dobré rozloženie rezíduí.
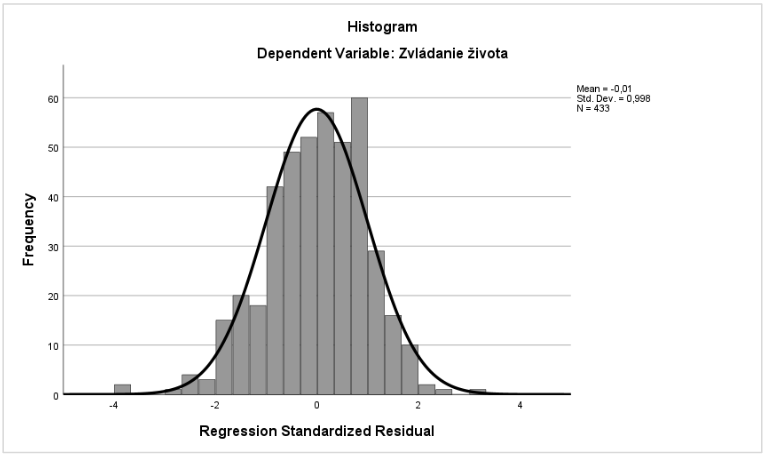
Graf 24 Histogram reziduí testujúci normálne rozloženie rezíduí závislej premennej
Predpoklad homoskedasticity sme overili prostredníctvom bodového grafu zobrazujúceho vzťah štandardizovaných rezíduí a štandardizovanej predikovanej hodnoty závislej premennej. Graf testuje konštantnosť rozloženia rezíduí v regresnom modeli, pričom môžeme potvrdiť zachovanie podmienky homoskedasticity (Graf 25)
Interpretácia výsledkov výskumnej otázky: Výskumná otázka bola testovaná použitím viacnásobnej lineárnej regresnej analýzy metódou postupného vkladania, jej výsledky uvádzame v Tabuľkách 22 a 23. Testovali sme predikčný potenciál optimizmu, sebaúcty, sociálnej žiadúcnosti a pohlavia voči zvládaniu života. V každom kroku boli pridané prediktory na základe hodnoty p (p ≤ 0,05), finálny regresný model môžeme vyjadriť prostredníctvom nasledovnej schémy: Zvládanie života = 8,226 + 0,324xOptimizmus + 0,230xSebaúcta – 0,828xPohlavie.
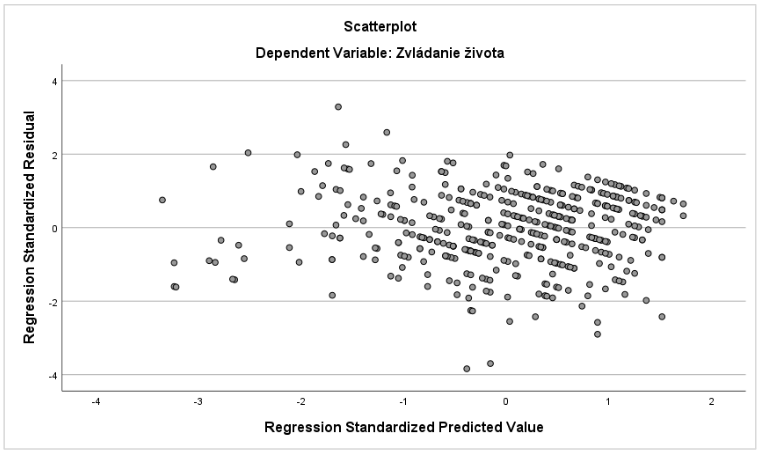
Graf 25 Bodový graf vzťahu štandardizovaných rezíduí a štandardizovanej predikovanej hodnoty závislej premennej
Kontrola predpokladov: Pred preskúmaním predikčnej sily regresného modelu sme posúdili všetky dôležité predpoklady, s cieľom potvrdiť adekvátnosť analýzy. Prostredníctvom bodových grafov sme overili linearitu prediktorov so závislou premennou a nezistili sme narušenie danej podmienky. Durbin -Watson koeficient dosiahol hodnotu 1,951, na základe čoho konštatujeme, že sa naplnila podmienka nezávislosti rezíduí. Faktor inflácie variancie (VIF) sa pri všetkých prediktoroch nachádzal pod prahom 5 (najvyššia hodnota dosahovala 1,496 pr e premennú sebaúcta), na základe čoho vyhodnocujeme, že všetky z významných prediktorov pridávajú unikátnu varianciu pri predikcii závislej premennej. Kontrola histogramu rezíduí a diagnostika prípadov naznačila, že sa v dátach nachádzajú vplyvné prípady, z toho dôvodu sme vykonali kontrolu vplyvu prípadov a nakoľko hodnoty DF Beta boli v prípade každého prediktoru menšie ako 0,096 (2/√N), usudzujeme, že prípady neovplyvnili stabilitu analýzy. Kontrolou bodového grafu štandardizovaných predikovaných hodnôt a rezíduí bola potvrdená homoskedasticita. Súhrnne tieto diagnostické testy potvrdili predpoklady, na ktorých je založený aktuálne testovaný viacnásobný lineárny regresný model, a poskytli tak solídny základ pre následnú analýzu.
Zhrnutie modelu: Celkový model je štatisticky významný, čo naznačuje F – štatistika o hodnote 88,029 a p menším ako 0,001 (F(2,429) = 88,029, p < 0,001), znamená to, že model vysvetľuje významnú časť rozptylu závislej premennej zvládanie života. Hodnota R² celkového modelu r ovnajúca sa 0,383 poukazuje na to, že testovaný regresný model predstavuje približne 38% rozptylu zvládania života. Zistili sme, že optimizmus ( β = 0,367; p = 0,001) pozitívne predikuje mieru zvládania života a vysvetľuje 29,7% jeho rozptylu. Sebaúcta ( β = 0,318; p = 0,001) taktiež pozitívne predikuje pocit zvládania života a vysvetľuje 7,5%. A napokon pohlavie ( β = -0,104, p = 0,007) významne negatívne predikuje zvládanie života, pričom vysvetľuje 1,1% rozptylu. Sociálna žiadúcnosť sa nepreukázala ako vysvetľujúca s ohľadom na sledovanú závislú premennú 40.
Tabuľka 23 Výsledky testovania výskumnej otázky: Viacnásobná lineárna regresná analýza (predikcia zvládania života)
| B | Beta | t | p | |
| Konštanta | 8,226 | , | 7,414 | ,001 |
| Optimizmus | ,0,324 | ,367 | 7,902 | ,001 |
| Sebaúcta | 0,230 | ,318 | 6,827 | ,001 |
| Pohlavie | -0,828 | -,104 | -2,724 | ,007 |
Pozn.: Metóda postupného vkladania, R 2 adj = 0,378.
ÚLOHY
- Sformulujte dvojsmernú a následne jednosmernú hypotézu, ktorá by testovala
predikčný vzťah medzi IQ, kompetentnosťou a efektivitou práce .
- Zamyslite sa, ktoré premenné by mohli predstavovať prediktory a ktorá premenná by mohla predstavovať závislú premennú.
- Sformulujte hypotézu/výskumnú otázku, ktorá by zisťovala predikčný potenciál
kardinálnej a nominálnej premennej voči kardinálnej premennej.
- Overte linearitu vzťahu medzi prediktorom a závislou premennou vo vlastnej databáze.
- Zohľadnite potrebné parametre (nezávislosť rezíduí, možnú kolinearitu, normalitu chýb merania, homoskedasticitu).
- Hypotézu/výskumnú otázku otestujte v štatistickom softwari, spracujte do tabuliek a interpretujte.
ZÁVEREČNÉ ÚLOHY
- Výskum je zameraný na súvislosť medzi neurotizmom a fajčením. Neurotizmus je
meraný 9 položkami dotazníka (Likertova škála), fajčenie je kardinálna premenná
(počet cigariet za mesiac), zahŕňa aj hodnotu 1 = nefajčenie (použite cvičný súbor).
- Formulujte a testujte jednosmernú korelačnú hypotézu (zvážte parametre typu premennej, prípadne normality pre voľbu testu). Výsledky spracujte do tabuľky, zobrazte príslušným grafom a interpretujte.
- Preskúmajte, či budú výsledky (korelácie) vecne rozdielne medzi mužmi a ženami (SPLIT FILE). Výsledky spracujte do tabuľky, tabuľku interpretujte, spravte príslušný graf pre obe podskupiny.
- Overte, či platí, že čím je fajčiar emočne labilnejší, tým fajčí viac cigariet (tzn. vyraďte z testovania nefajčiarov – SELECT CASES). Zhodnoťte typ premenných, normalitu (ak je potrebné), zvoľte správny test. Výsledky spracujte do tabuľky, interpretujte a vypracujte graf.
- Formulujte hypotézu o rozdiele v neurotizme medzi fajčiarmi a nefajčiarmi (je potrebné RECODE-ovať súbor na tieto dve skupiny, preskúmať normalitu v oboch skupinách), zvoľte správny komparačný test, výsledky spracujte do tabuľky, interpretujte, vypracujte príslušný graf (napr. boxplot)
- Formulujte hypotézu o súvislosti, že fajčiari sú skôr emočne labilní než nefajčiari (obe premennú sú tu kategorické), použite nasledujúc e kroky:
- Rekódujte kardinálnu premennú Neurotizmus na tri kategórie: nízke, stredné a vysoké skóre, kde stredné pásmo bude reprezentovať M ± ŠO (je potrebné najskôr spraviť deskripciu a zistiť priemer, štd.odchýlku, určiť hraničné hodnoty pásiem, potom rekódovať do NEW VARIABLE).
- Odfiltrujte z vyhodnotenia stredné pásmo Neurotizmu (použite SELECT CASES – odfiltrujte stredné pásmo alebo RECODE – vytvorte novú premennú s dvoma kategóriami).
- Sformulujte pracovnú komparačnú jednosmernú hypotézu s určením, v ktorej skupine bude vyššie/nižšie zastúpenie (početnosti) jednej či druhej kategórie Neurotizmu.
- Sformulujte pracovnú hypotézu o závislosti (vzťahu) medzi kategorickými premennými (ak sa to podarí správne, nebude znieť ako hypotéza na korelačný lineárny vzťah).
- Hypotézy testujte príslušným testom (na báze krížovej tabuľky) , tabuľky upravte podľa vzoru, interpretujte, vytvorte príslušný graf.
- Vymyslite analogický príklad (ako v úlohe 24) s použitím iných premenných cvičného súboru alebo vlastného súboru (premenná A a premenná B), obe premenné môžu byť kardinálne, alebo jedna ordinálna (aby ich bolo možné rekódovať na tri/dve kategórie) a aby predpoklady o súvislostiach (rozdieloch vzťahoch) mali zmysel z hľadiska psychológie.
- Formulujte a testujte jednosmernú korelačnú hypotézu (zvážte parametre typu premennej, prípadne normality pre voľbu testu). Výsledky spracujte do tabuľky, zobrazte príslušným grafom a interpretujte.
- Preskúmajte, či budú výsledky (korelácie) vecne rozdielne medzi mužmi a ženami (alebo inými skupinami, SPLIT FILE). Výsledky spracujte do tabuľky, tabuľku interpretujte, spravte príslušný graf pre obe podskupiny.
- Overte, či platí súvislosť medzi premennou A a B iba v nejakej špecifickej skupine zo súboru (tzn. použite filter s určením skupiny, SELECT CASES). Zhodnoťte typ premenných (v rámci týchto filtrovaných dát), normalitu (ak je potrebné), zvoľte správny test. Výsledky spracujte do tabuľky, interpretujte a vypracujte graf.
- Formulujte hypotézu o rozdiele v A medzi skupinami podľa B (je potrebné RECODE-ovať súbor na skupiny, preskúmať normalitu v oboch skupinách), zvoľte správny komparačný test, výsledky spracujte do tabuľky, interpretujte, vypracujte príslušný graf (napr. boxplot).
- Formulujte hypotézu o súvislosti, že jedna skupina podľa B premennej vykazuje viac z nejakej kategórie premennej A (obe premennú sú tu kategorické), použite nasledujúce kroky ako v predchádzajúcej úlohe.

